한동안 개인 사정으로 인해 다른 일을 할 수 없어 Google Code Jam 본대회 Qualification Round를 불참했는데, 마침 오늘 Code Jam Kickstart 가 있길래 참가해봤다.
Kickstart는 CodeJam 본대회와 달리 비교적 자주 진행되고(2017년 기준 7회), 다양한 시간대에 분포해 있어 코포처럼 새벽까지 깨어있지 않아도 참가할 수 있다. 대회 자체적으로 상을 주지는 않지만 좋은 성적을 낼 경우 구글에서 인턴/입사 인터뷰 메일이 오기도 하니 시간이 된다면 참가해보자. 실제로 2017년 Kickstart Round G 때 15등 찍어서 메일 받아봄.
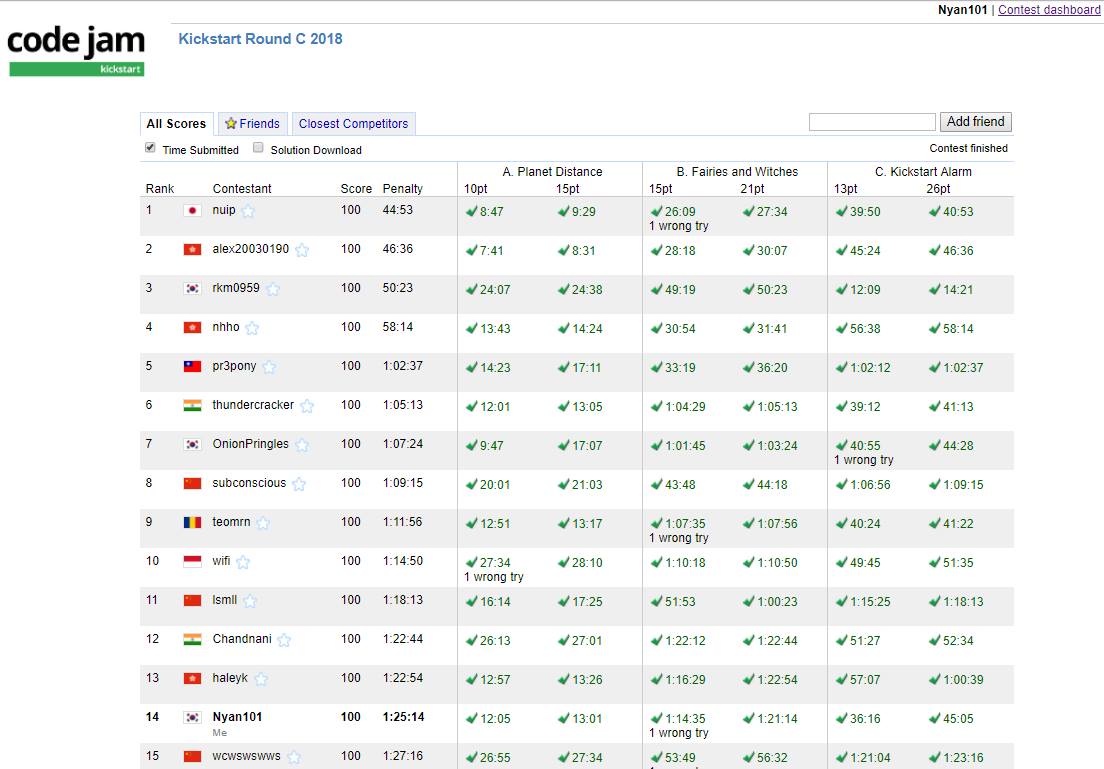
한동안 코딩을 하지 않아 걱정했는데 다행히 풀이들이 비교적 금방 떠올랐고, 최종 14등으로 대회를 마칠 수 있었다.
문제는 여기 에서 볼 수 있다. 어차피 며칠 후면 analysis가 올라오겠지만 내 풀이를 간단히 적어봤다.
Problem A. Planet Distance
사이클이 하나 있는 그래프가 주어지면, 각 정점에서 사이클까지의 거리를 구하는 문제이다. Cycle-Detection을 진행하고 어떤 정점들이 사이클에 속하는지 구해 BFS를 돌리면 된다. 코딩이 조금 까다로울 것이라 생각했으나 Large의 N제한이 1000인 걸 보고 그냥 O(N^2)으로 구현했다.
Problem B. Fairies and Witches
주어진 그래프의 각 간선이 막대라고 가정하자. 이들 중 다음을 만족하는 막대들의 집합의 수를 구하는 문제이다.
- 집합의 어떤 두 막대도 원 그래프에서 인접(=끝점을 공유)하지 않는다.
- 집합의 막대들을 모두 사용해 넓이가 0이 아닌 Convex Polygon을 만들 수 있다.
이중 Convex Polygon에 대한 두 번째 조건은 다음과 같이 바꿀 수 있다.
- 집합에 속한 막대의 수가 3 이상이다.
- 집합에 속한 막대의 총 길이 합은 가장 긴 막대길이의 2배를 넘어야 한다.
이제 첫 번째 조건을 만족하는 집합을 생성하고 위 조건을 고려하면 된다. 이는 N제한이 Small에서 6, Large에서 15로 주어졌기에 완전탐색으로 풀 수 있다고 생각했다. Small의 경우 O(2^E)로도 가능했으나 Large를 해결하기엔 약간 부족했고, 집합에서 “간선끼리 공유하는 정점이 없다” = “각 정점에서 최대 하나의 인접간선만 뽑을 수 있다"는 점에 착안해 고려해야 하는 경우의 수를 크게 줄일 수 있었다.
Problem C. Kickstart Alarm
문제 링크에 공식이 나와 있어 따로 작성하지는 않는다. 주어진 공식으로 POWER_i라는 값이 정의될 때, i가 1~K까지 모든 POWER의 합을 구하는 문제이다. 식을 정리하면 결과적으로 다음을 구하라는 문제로 바뀐다.
A[1], A[2], …, A[N]에 대해
A[i] x (N-i+1) x ( (1^1+1^2+…+1^K) + (2^1+2^2+…+2^K) + … + (i^1+i^2+…+i^K))
들의 합을 구하라.
a^1 + a^2 + a^3 + … + a^K를 등비수열의 합 공식을 써 구할 수 있다는 것만 파악하면 O(N logK)에 해결할 수 있다.
해당 라운드의 최종 스코어보드 에서 각 참가자가 작성한 코드를 다운받을 수 있으니 참고하자.