코드잼이 새로운 시스템으로 바뀌었다. 사실 메인 코드잼에선 작년에 도입된 시스템이 올해 킥스타트까지 적용된 거라고 하는데 작년 코드잼은 국방부 전직퀘스트를 해야 했어서 개인적인 사정으로 참가를 못했으니 이번이 새로운 시스템을 경험하는 첫 대회였다.

결론부터 말하면 다소 삐걱거리는 출발이었다. 시작 직후 한동안 문제 로딩이 안 되면서 몇 분 후에야 문제를 볼 수 있었고, 제출에서도 다소의 딜레이가 있었다. 거기에 더해 대회 막판에는 아예 제출버튼을 눌러도 코드 제출이 이루어지지 않아서 결국 끝까지 제출하지 못한 상태로 대회가 끝났다. 나름 지난 몇 차례의 킥스타트에서 꾸준히 10~20등 정도의 성적을 내다가 이번에 299등이라는 숫자를 보니 조금 억울하긴 하다(…)

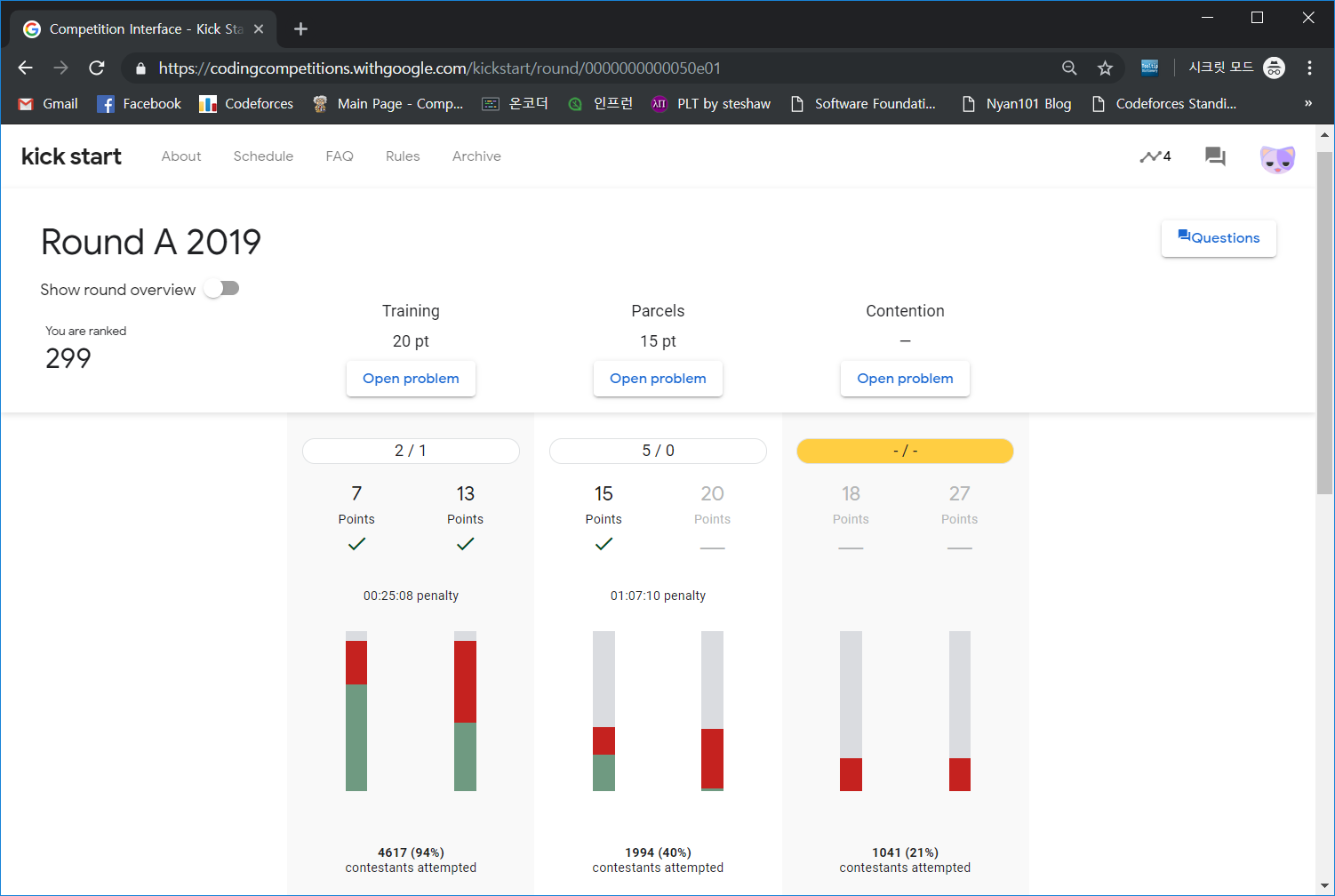
문제 난이도는 작년보다 상당히 어려워졌다고 느꼈다. 하지만 input.txt를 다운받아 output.txt를 제출하는 예전 방식과 달리 코드 자체를 제출하게 되면서 (채점 데이터가 공개되지 않으니) 틀려도 여러 번 다시 제출할 수 있도록 바뀌었는데, 이 덕분인지 다소 가벼운 마음으로 진행할 수 있었다. 전체 문제는 여기에서 풀어볼 수 있다.

Problem A. Training

구성된 fair team의 스킬 레벨 S가 고정되었을 때 필요한 최소 코칭시간을 구하는 건 간단하다. S이하의 스킬레벨을 가지는 학생들 중 기존 레벨이 높은 순서대로 P명을 고르고, 선택된 학생들을 S까지 끌어올리는 게 최적임은 쉽게 보일 수 있다. 이때 선택된 P명 중 레벨이 i인 학생의 수를 cnt[i]라고 하면

\[cost = \sum_{i=1}^{S} (S - i) * cnt[i]\]

가 된다. 그런데 이를 직접 구하면 \( O(S_{max}) \)가 되므로 전체 복잡도는 \( O({S_{max}}^2) \)이 된다. S의 범위가 1만 이하이므로 이대로도 아슬아슬하게 가능할지 모른다. 그렇지만 미리 전체 학생에 대해 각 레벨별 인원수 cnt[i]와 (Smax-i)*cnt[i]를 전처리로 구해놓으면 prefix sum과 two-pointer 기법을 종합해 각 S에 따른 cost를 매번 amortized O(1)에 구할 수 있다. 이때 정확히 P명을 선택해야 하므로 prefix sum으로부터 cost를 계산할 때 보정해야 하는 항에 주의하면 전체 \( O(S_{max}) \) 의 시간복잡도로 문제를 해결할 수 있다. [source]

Problem B. Parcels

Small은 모든 경우에 대해 BFS를 수행해보는 완전탐색으로 구할 수 있다. 이때 시간복잡도는 \( O((R*C)^2) \)이 되고 R,C가 최대 10이므로 충분히 적용 가능하다. Large는 R,C가 각각 250 이하이므로 다른 접근이 필요한데, 처음에 방법이 쉽게 떠오르지 않아서 일단 Small 전용 코드를 먼저 제출했다.

Large를 해결하는 데 있어서 핵심 아이디어는 새로운 오피스가 담당할 수 있는 영역은 다이아몬드 형태라는 점이다. 두 점 \( (x_1,y_1), (x_2,y_2) \) 사이의 거리가 \( |x_1 - x_2| + |y_1 - y_2| \) 로 정의되므로 새로운 오피스에서 거리가 K 이하인 영역들은 다이아몬드 형태를 가질 수밖에 없다. 따라서 이를 역으로 이용해 전체 \(R*C\) 개 영역을 1)기존 오피스들이 담당하는 영역과 2)새로운 오피스가 담당할 영역으로 나누고, 주어진 영역들을 커버할 수 있는 가장 작은 다이아몬드의 크기를 구하는 방법을 생각할 수 있다.

이제 이를 다이아몬드를 구성하는 \(y=x+a\) 와 \(y=-x + b\) 직선을 구하는 것으로 바꿔 생각해보자. 다시 말해, 주어진 집합을 구성하는 지점들에 대해 \( x-y, x+y \)의 최대,최소값을 찾고 그 점들을 모두 커버하는 다이아몬드를 구하면 된다. 아래 그림을 참고하자.

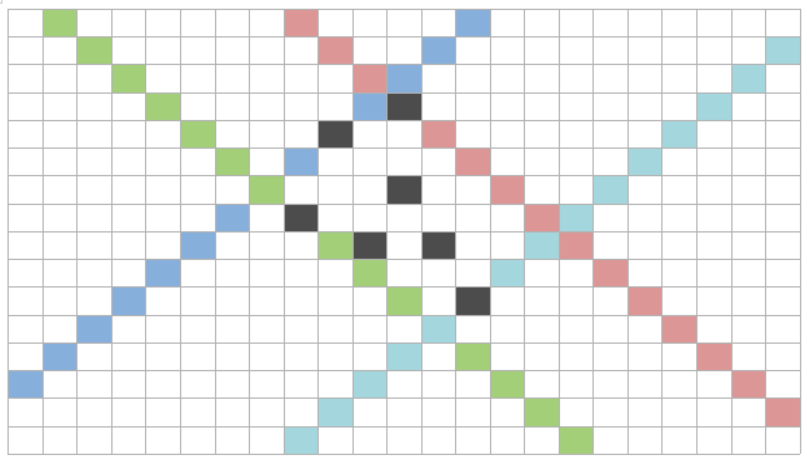
여기서 검은색 영역을 모두 커버하는 다이아몬드를 찾는다고 하자. x+y가 최대,최소인 지점과 x-y가 최대,최소인 지점에서 사선을 그리고, 그중 더 길이가 긴 변을 최종 다이아몬드의 크기로 삼으면 된다. 사전에 모든 x+y, x-y의 경우의 수를 카운트한 후, 기존 오피스들로부터 BFS를 통해 “기존 오피스가 담당하는 영역”을 점차 확장시키면서 새로운 오피스가 담당해야 할 영역의 크기를 구해 최종 답을 구할 수 있다. x+y, x-y의 범위가 500 이내이므로 배열에 모든 경우의 수를 담을 수 있다. 여기에 집합에서 원소가 제거될 때 최대,최소값은 각각 감소,증가하기만 한다는 사실을 이용하면 BFS를 수행하면서 남아있는 x+y, x-y의 최대,최소를 amortized O(1)에 구할 수 있다. 여기에 분홍색 사선과 같이 엇갈리게 교차되는 경우에 주의하면 전체 시간복잡도 \( O(R*C)\) 에 문제를 해결할 수 있다. [source]

그렇게 코딩을 끝내고 B Large에 다시 제출버튼을 눌렀지만 제출이 안 됐다.. 처음엔 채점 횟수에 제한이 있거나 내 인터넷 환경의 문제인 줄 알았지만 public QnA를 통해 서버 차원에서의 문제라는 걸 알 수 있었다. 분 단위로 새로고침을 누르면서 차분히 서버가 복구되길 기다렸지만 결국 대회 종료까지 해결되지 않았고, 그렇게 B small까지 맞춘 323등으로 대회가 끝났다.

이후 Practice 모드에서 다시 채점해 본 결과 정답 판정을 받았다(…) 대회 당시에 B Large까지 통과한 사람의 수가 많지 않아 마지막 제출에 성공했다면 좀더 높은 등수를 받았을 거라는 아쉬움이 남지만 적어도 시간 내에 풀이를 떠올릴 수는 있었다는 점에서 만족하기로 했다. C는 Small에서도 아무런 아이디어가 떠오르지 않았는데 에디토리얼 올라오면 한번 읽어봐야겠다.