Coq 02 - 자연수 덧셈의 결합법칙 증명

대부분의 reference가 그렇듯이 읽다보면 쉽게 지루해진다. 지루함을 덜하고 Coq에 익숙해지기 위해 일단 예제를 조금씩 따라해보면서 익혀가기로 했다. 자바를 처음 배울 때 public static void main(int argv, char **argc)가 정확히 뭔지는 몰라도 “Hello World” 부터 찍어보는 그런 마음으로 진행해봤다.

CoqIDE 실행

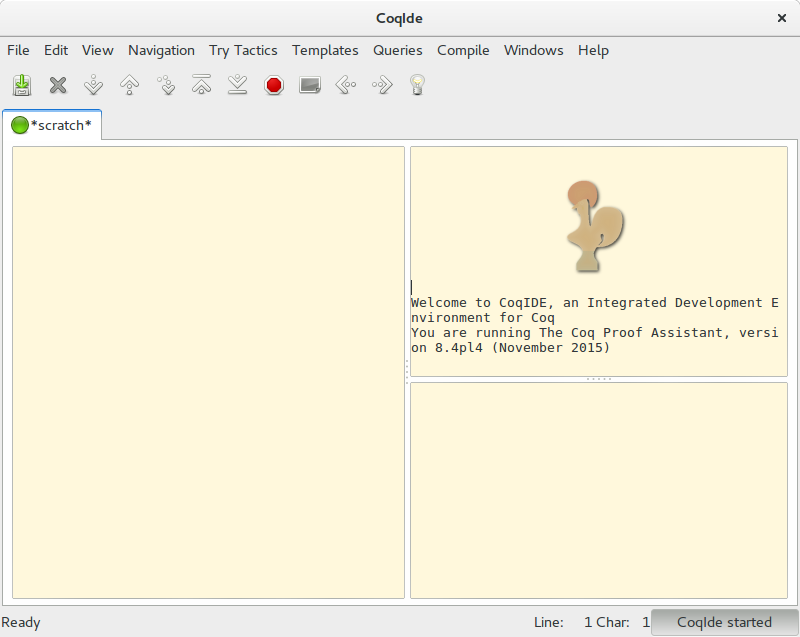
프로그램을 처음 실행하면 다음과 같은 화면을 볼 수 있다. 크게 3가지 창으로 나뉘어져 있으며, 왼쪽은 코드 작성을, 오른쪽 위/아래는 각각 Proof 보조/결과 출력을 담당하는 역할이었다.

coqIDE

자연수 집합 mynat 정의

이제 자연수 집합을 정의해보자. 사실 Coq에서는 이미 nat이라는 형태로 자연수를 제공하지만, 여기서는 mynat이라는 이름으로 처음부터 정의해나가기로 하자. 자연수 집합은 아래와 같이 Inductive하게 정의할 수 있다.

Inductive mynat : Set :=
 | O : mynat
 | Succ : mynat->mynat.

위 코드를 한줄씩 살펴보자

Inductive mynat : Set := “mynat이라는 집합(Set)을 Inductive하게 정의하자”
O : mynat “O(숫자 0이 아닌 알파벳 O임에 유의)은 mynat에 속한다”
Succ : mynat->mynat “Succ은 mynat 에서 mynat으로 가는 함수이다.”

🡒 어떤 x가 mynat에 속한다면, (Succ x) 도 mynat의 원소이다.

Coq의 모든 statement는 .(period)으로 끝난다는 점에 유의해야 한다.

여기서 Succ 함수는 보통 “다음 자연수를 제공하는 함수”로 해석해 (Succ 0) = 1, (Succ 1) = 2, … 등으로 해석되지만 이는 반대로 이해해야 한다. 코드의 Succ 정의로부터 알 수 있는 사실은 오직 “x가 mynat일 때 (Succ x)도 mynat이다”라는 점일 뿐 자연수들 사이의 순서에 대해서는 말하지 않았다. 오히려 1, 2, 3을 각각 (Succ O), (Succ 1)(혹은 (Succ (Succ O))), (Succ (Succ (Succ O)))을 나타내는 syntactic sugar라고 받아들이는 편이 더 적절하다.

여기까지 실행시키면 오른쪽 아래 창에 다음과 같은 출력을 볼 수 있다.

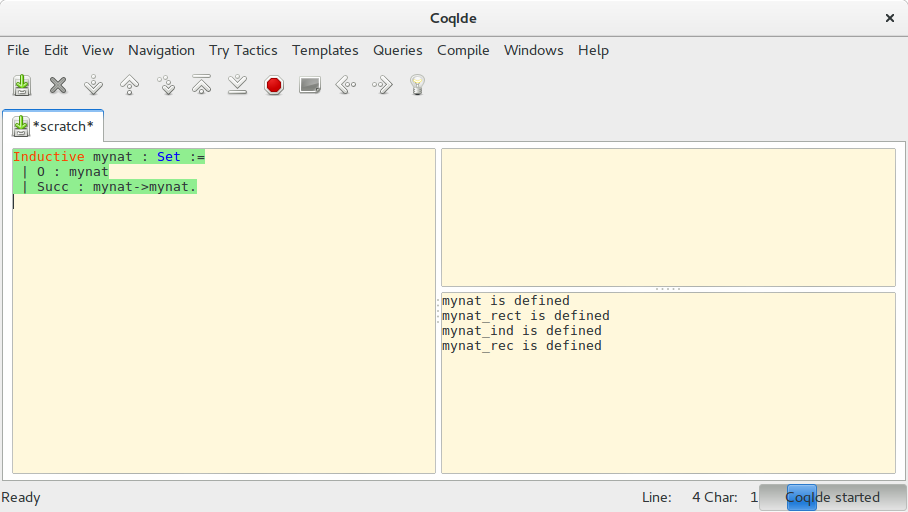
mynat_definition

분명 mynat만 정의했는데 mynat_rect, mynat_ind, mynat_rec이라는 것들이 함께 정의된 것을 볼 수 있다. 이는 Inductive 키워드를 사용해 귀납적으로 mynat을 정의한 결과인데, 잠시 후 덧셈의 결합법칙 증명에서 이를 사용할 것이다.

mynat에서의 덧셈 정의

“덧셈의 결합법칙”을 말하기 위해선 먼저 덧셈이 무엇인지부터 정의해야 한다. 덧셈은 mynat 에 속하는 인자 2개(a, b)를 받는 함수로 다음과 같이 정의될 수 있다.

Definition add (a b : mynat) :=
 match a with
 | O => b
 | Succ c => Succ (add c b)
 end.

코드에서 match a with ... 부분을 풀어 쓰면 아래와 같다. 앞서 Succ의 해석에 유의하자는 말을 했으나 여기서는 편의상 ‘다음 수’라는 용어를 사용했다.

0 => b 0 과 b를 더한 결과는 b이다
Succ c => Succ (add c b) a가 어떤 mynat (c라고 하자)의 ‘다음 수’였다면 a와 b를 더한 결과는 ‘(c와 b를 더한 결과)의 다음 수’가 된다.

그런데 실제로 위 코드를 실행하면 Error: The reference add was not found in the current environment. 라는 에러가 발생한다. add의 정의에서는 아직 add가 정의되지 않았기 때문인데, Definition 대신 Fixpoint를 사용해 해결할 수 있다.

덧셈의 결합법칙 증명

이제 “덧셈의 결합법칙이란 무엇인가”를 서술하는데 필요한 재료가 모두 갖추어졌다. 알다시피 결합법칙은 (a+(b+c))=((a+b)+c) 를 의미하며, 아래 코드에 이를 Theorem으로 서술했다. 증명해야 할 내용이 오른쪽 위에 subgoals라는 이름으로 나타난 것을 확인할 수 있다.

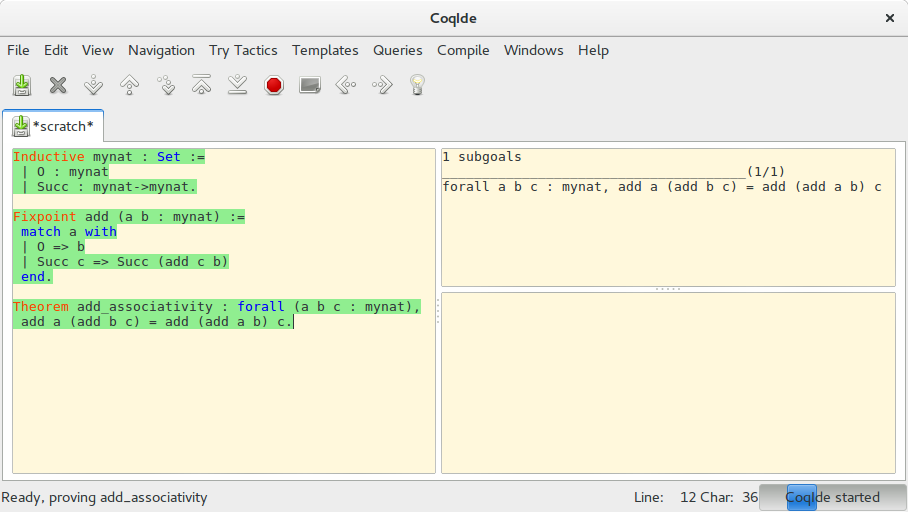
Coq_add_assoc_theorem

이제 증명을 시작하자. mynat에 속하는 모든 원소 a b c에 대해 (a+(b+c))=((a+b)+c)임을 보이려면 어떻게 해야 할까? 가장 처음은 mynat에 속하는 a b c가 주어졌다고 가정하는 것에서 시작한다.

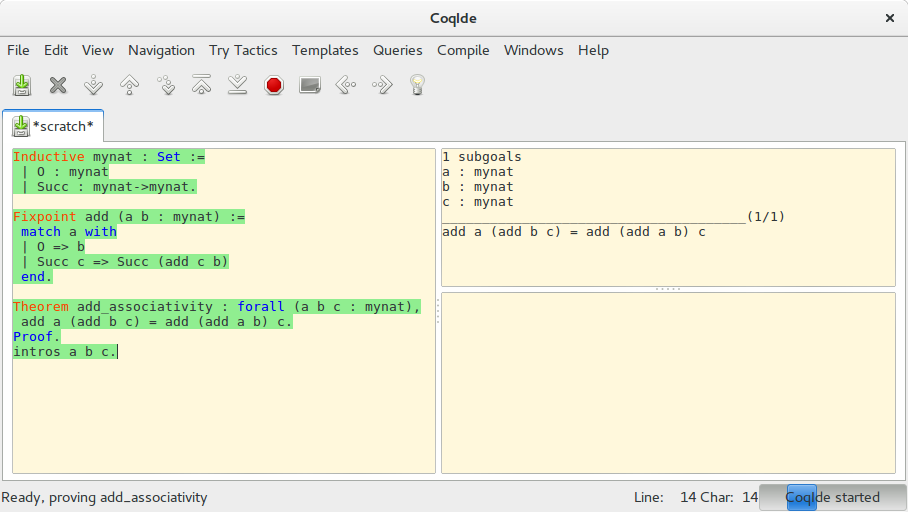
coq_add_assoc_proof_01

이제 a에 대해 수학적 귀납법을 적용하자. 앞서 mynat을 Inductive하게 정의했으므로 Coq는 이를 인식해 수학적 귀납법을 위한 틀을 제공해준다. subgoals를 보자.

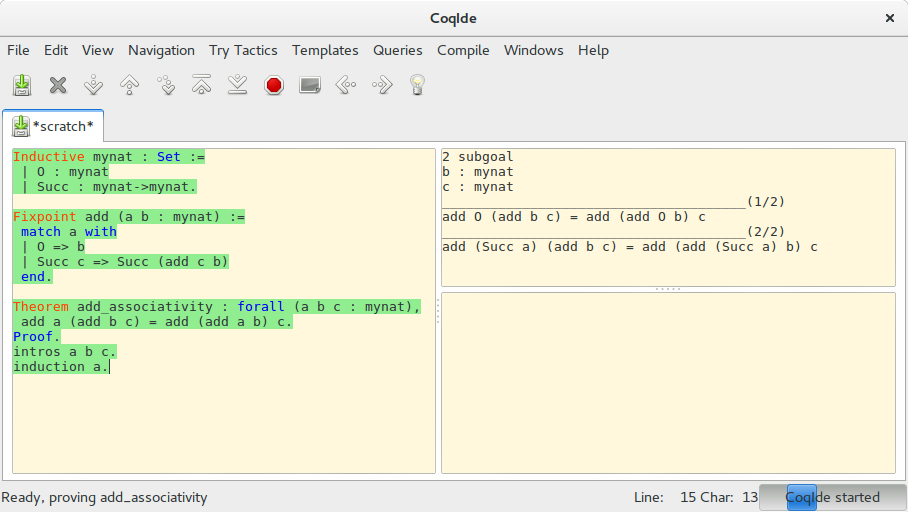
coq_add_assoc_proof_02

이제 subgoal들을 하나씩 보이자. simpl. 을 사용해 첫 subgoal을 간단히 하면 다음과 같이 변한다.

2 subgoal
b : mynat
c : mynat
______________________________________(1/2)
add b c = add b c
______________________________________(2/2)
add (Succ a) (add b c) = add (add (Succ a) b) c

~~딱 보면 왼쪽이랑 오른쪽이 같은데 왜 아직 안 끝났지~~ reflexivity. 다시 말해 x=x는 참이라는 사실을 이용하자. 그러면 subgoal이 하나 해결되고 Induction Hypothesis가 추가된 것을 확인할 수 있다.

1 subgoals
a : mynat
b : mynat
c : mynat
IHa : add a (add b c) = add (add a b) c
______________________________________(1/1)
add (Succ a) (add b c) = add (add (Succ a) b) c

다시 simpl.을 적용하자.

1 subgoals
a : mynat
b : mynat
c : mynat
IHa : add a (add b c) = add (add a b) c
______________________________________(1/1)
Succ (add a (add b c)) = Succ (add (add a b) c)

subgoal을 보면 어디서 많이 ~~그러니까 IHa같은 데서~~ 본 형태가 나타났다. rewrite -> IHa.를 이용해 IHa의 좌변을 모두 우변으로 바꿔 써 보자.

1 subgoals
a : mynat
b : mynat
c : mynat
IHa : add a (add b c) = add (add a b) c
______________________________________(1/1)
Succ (add (add a b) c) = Succ (add (add a b) c)

조금 전과 같이 reflexivity.를 사용하면 no more subgoals 라는 안내를 볼 수 있다. 이제 Qed.로 증명을 끝내면 add_associativity is defined 라는 메시지가 나오면서 증명이 완료된 것을 확인할 수 있다. 완성된 증명을 Print로 살펴보자.

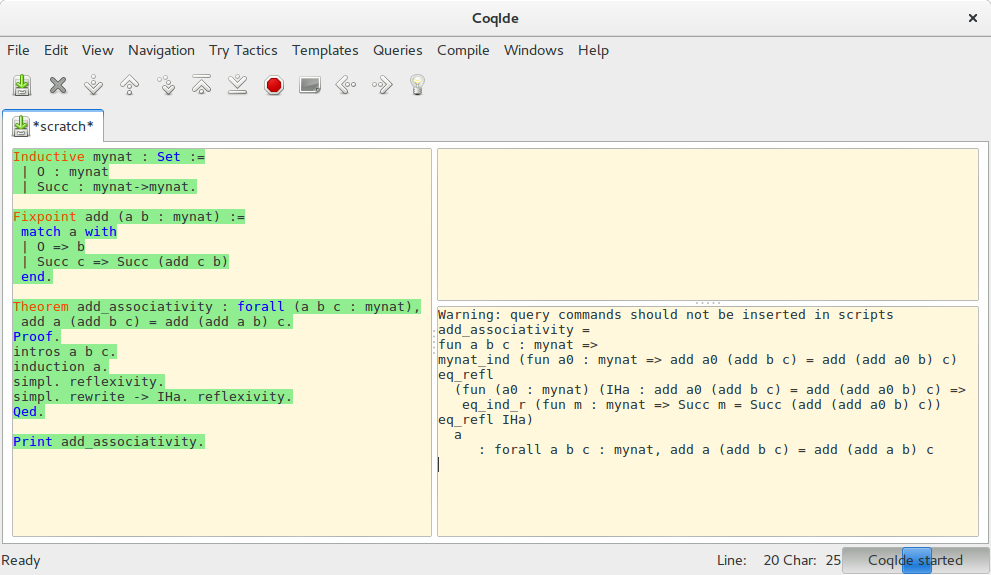
coq02_add_assoc_qed

증명 대신 fun 키워드로 시작하는 함수가 나타났다. 이는 프로그램과 (그 프로그램의) 타입 사이의 관계는 증명과 (그 증명이 증명하는) 명제 사이의 관계에 대응될 수 있다 라는 Curry-Howard isomorphism과 관련이 있다고 하는데, 이에 대해서는 차차 공부해나가기로 하자.