Möbius 함수의 정의와 활용

얼마 전 코드포스에서 흥미로운 문제를 접했다. 대회 당시에는 풀지 못했는데, 에디토리얼을 읽어보던 중 뫼비우스 함수(Möbius function)에 대한 언급이 있어 이에 대해 좀더 자세히 알아보았다.

Möbius function의 정의

뫼비우스 함수(Möbius function)는 자연수 n에 대해 다음과 같이 정의된다. ( $p$ 는 소수)

$\mu(n) = \begin{cases} (-1)^k & \mathrm{if\,\,\,\,} n=p_1p_2\cdots p_k \, (p_i \neq p_j)\\ 0 & \mathrm{if\,\,\,\,} p^2 | n \end{cases}$

다시 말해, n이 서로 다른 k개 소수들의 곱이면 $\mu(n)$ 은 $(-1)^k$ 이, 중복 소인수가 있으면(=어떤 제곱수를 약수로 가지면) 0이 되는 함수라고 할 수 있다. (이때 $\mu(1)=1$ )

뫼비우스 함수의 정의를 살펴보면 두 자연수 a,b에 대해 다음 성질이 성립함을 쉽게 알 수 있다.

$\mu(ab) = \mu(a)\mu(b) \,\,\,\,\mathrm{if\,}\gcd(a,b)=1$

이밖에도 다양한 성질들이 있지만 이번 글에서는 알고리즘적 측면에서의 활용에 집중하기로 한다.

포함-배제의 원리

다음 벤 다이어그램을 살펴보자.

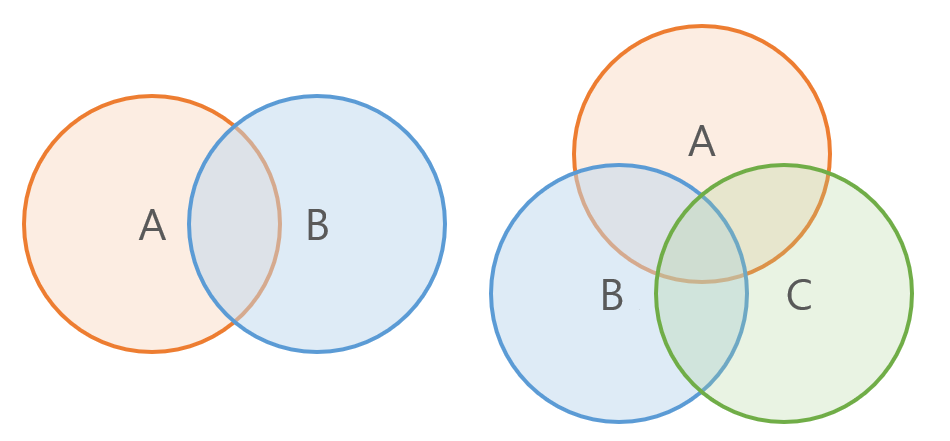
전체 합집합의 넓이는 어떻게 구할 수 있을까? 색칠을 해보면 다음 식을 어렵지 않게 구할 수 있다.

$\begin{array}{cl} |A \cup B| & = &|A| + |B| - |A \cap B|\\ |A \cup B \cup C| & = &|A| + |B| + |C| - |A \cap B| - |B \cap C| - |C \cap A| + |A \cap B \cap C| \end{array}$

같은 원리를 확장하면 n개 집합에 대해 다음을 얻을 수 있다.

$\begin{aligned}\\{\biggl |}\bigcup _{i=1}^{n}A_{i}{\biggr |}&{}=\sum _{i=1}^{n}\left|A_{i}\right|-\sum _{i,j\,:\,1\leq i<j\leq n}\left|A_{i}\cap A_{j}\right|\\&{}\qquad +\sum _{i,j,k\,:\,1\leq i<j<k\leq n}\left|A_{i}\cap A_{j}\cap A_{k}\right|-\ \cdots \ +\left(-1\right)^{n-1}\left|A_{1}\cap \cdots \cap A_{n}\right|\end{aligned}$

이를 포함-배제의 원리라고 한다.

약수 관계에서의 포함-배제의 원리

이제 이를 약수-배수 관계에서 생각해보자. 자연수 n이 주어졌을 때 $S_n$ 을 정의할 수 있고, m이 n의 배수일 때 $S_m \subset S_n$ 이 성립한다고 하자. 다시 말해, 각 집합끼리의 포함관계가 약수-배수 관계에 따라 정해지는 상황이다. 잘 와닿지 않는다면 간단히 $S_n$ 을 (max 이하의 자연수들 중) $n^2$ 의 배수들의 집합¹이라고 가정하고 읽어보자. 모든 자연수 n에 대해 $|\bigcup _{i=2}^{n}S_{i}|$ 를 구하려면 어떻게 해야 할까?

먼저 다음과 같은 성질을 알 수 있다.

자연수 $a$ 에 대해 $S_a$ 를 고려했으면 $S_{a^2}, S_{a^3}$ 등은 고려할 필요가 없다
$\bigcup _{i=2}^{n}S_{i}$ 은 소수 $p_i$ 들만을 고려한 $\bigcup _{p_i} S_{p_i}$ 와 같다.

그렇다면 포함-배제의 원리에 따라 $\left|\bigcup _{i=2}^{n}S_{i}\right|$ 는 다음과 같이 구할 수 있다.

소수 $p_i$ 들에 대해 $\sum_i \left| S_{p_i} \right|$ 를 구해 더한다
$i < j$ 에 대해 $\sum_{i<j} \left| S_{p_i} \cap S_{p_j} \right|$ 를 구해 뺀다
$i < j < k$ 에 대해 $\sum_{i<j<k} \left| S_{p_i} \cap S_{p_j} \cap S_{p_k}\right|$ 를 구해 더한다
(이하 반복)

고려해야 할 경우의 수가 작으면 $O(2^n)$ 복잡도를 가지는 알고리즘으로 전체 경우의 수를 구할 수 있다. 그러나 수가 증가할수록 모든 경우를 고려하는 복잡도는 크게 증가한다. 뫼비우스 함수를 이용하면 이와 같은 포함-배제를 비교적 간단히 처리할 수 있다.

$\left|\bigcup _{i=2}^{n}S_{i}\right| = -\sum_{i=2}^{n} \mu(i)|S_{i}|$

여기서는 단순히 집합의 크기만을 고려했지만 $S = \bigcup _{i=2}^{n}S_{i}$ 에 대해 소속 원소의 함수값들의 aggregation을 구하는 경우, 즉 $\sum_{x \in S} f(x)$ 나 $\prod_{x \in S} f(x)$ 를 구하는 상황으로도 어렵지 않게 확장할 수 있다.

프로그래밍 언어로의 구현 (C++)

마지막으로 mu의 계산에 대해 알아보자. 주 원리는 다음과 같다.

모든 자연수 s는 m×p 형태로 표현할 수 있다. (p는 s의 가장 작은 소인수)
- 이때 m이 p의 배수이면 s는 제곱수를 인자로 가진다.

그러면 n 이하의 소수 리스트 vector<int> pvec을 이용해 다음과 같이 int mu[n] 배열을 채울 수 있다.

int  mu[n+1];
bool isPrime[n+1];
vector<int> pvec;

fill(isPrime, isPrime+n+1, true);
fill(mu, mu+n+1, -1);

mu[1] = 1;
for(int i=2;i<=n;i++)
{
    if(isPrime[i])
        pvec.push_back(i);

    for(int p : pvec)
    {
        if(i*p > n) break;
        
        isPrime[i*p] = false;
        
        if(i%p == 0)
        {
            mu[i*p] = 0;
            break;
        }
        mu[i*p] = mu[i]*mu[p];
    }
}

연습문제

[BOJ 1557번] 제곱 ㄴㄴ

본문에서 예시로 든 상황과 정확히 같다. “K 이하의 제곱 ㄴㄴ수”가 아닌 “K번째 제곱 ㄴㄴ수”임에 유의하자.
[Codeforces] D. Steps to One (Round #548, Div.2)

포함배제를 O(2^n)에 진행할 수도 있지만 뫼비우스 함수와 Linearity of Expectation을 이용해 해결하는 풀이가 존재한다. “마지막 (1이 아닌) gcd가 k의 배수였을 때, 길이의 기대값”을 생각해보고 k=6인 상황은 k=2인 경우와 k=3인 경우 양쪽으로 해당될 수 있다는 점을 염두에 두면서 풀어보자.

단순히 “n의 배수들의 집합”이라고 할 수도 있지만, 그 경우 $\bigcup _{i=2}^{n}S_{i}$ 이 지나치게 단순해지므로 그보다는 약간 복잡한 정의를 선정. ↩