[Coq 입문] Ch01. Functional Programming in Coq (2)

Define Numbers

이전 글에서는 day, bool, color 와 같이 원소의 개수가 유한한 타입, 다시 말해 타입 \(T\)에 대해 \(\{x | x \mathrm{\,has\,type\,}T\} \)가 유한집합인 경우만을 다뤘다. 무한한 원소를 가지는 타입을 정의하려면 어떻게 해야 할까? 집합론에서와 마찬가지로 자연수에서 시작해보자. 페아노 공리계(Peano axioms)에서 필요한 부분을 빌려오자. 크게 중요하지 않은 공리들은 생략했다

1. 0 is a natural number.

5. For every natural number n, S(n) is a natural number.

이제 이 정의를 그대로 Coq로 옮겨보자.

Inductive nat : Type :=
| O
| S (n : nat).

이제 O, S 0, S (S 0), S (S (S 0))으로 이어지는 모든 패턴은 nat 타입이 된다. 위 코드는 실제 Coq에서 자연수 nat이 정의되는 방식과 동일하다. 정의를 살펴보면 O, S 0, S (S 0), S (S (S 0)), …이 각각 0, 1, 2, 3, …에 대응된다는 사실을 쉽게 눈치챌 수 있다. Coq에서는 이를 반영해 S (S (S ...)) 대신 알아보기 편한 syntactic sugar를 제공한다. 이를 적용하기 위해 앞서 작성한 nat 정의를 지우고 Check로 확인해보자.

>> Check (S (S (S (S O)))).

   4 : nat

이제 nat 타입을 받는 함수를 만들어보자. predecessor 함수 pred는 다음과 같이 정의할 수 있다.

Definition pred (n : nat) :=
match n with
| O => 0
| S n' => n'
end.

0의 predecessor는 0으로 정의했음에 유의하자(결과물도 nat 범위 안에 있으려면 -1은 나올 수 없다). 마찬가지로 minusTwo 함수를 만들 수 있다.

Definition minusTwo (n : nat) :=
match n with
| O => O
| S O => O
| S (S n') => n'
end.

Compute를 통해 함수가 의도한 대로 만들어졌는지 확인하자.

>> Compute (pred 4).

   3 : nat
>> Compute (minusTwo 4).

   2 : nat
>> Check minusTwo.

   minusTwo : nat -> nat

여기서 한 가지 짚고 넘어가야 할 사실이 있다. pred, minusTwo, S 모두 Check를 통해 확인해보면 nat -> nat 타입으로 동일하고, S도 나머지 둘과 마찬가지로 Compute가 된다.

>> Compute (S 3).

   4 : nat

하지만 S는 pred, minusTwo와 근본적으로 다르다. 구체적으로 pred는 일종의 계산규칙(computation rule)을 가지고 nat 위에서 정의된 함수이고 S는 nat의 정의에서 등장하는 생성자라는 차이를 가진다. pred의 정의에 따라 pred 4는 3으로 simplified될 수 있지만 S 3이 4가 되는 건 Coq에서 제공하는 syntactic sugar일 뿐 simplified가 아니다. 잠시 10진법을 머리에서 지우고 S와 O을 이용한 표기로 돌아가보면 그 차이를 이해할 수 있다.

>> Compute (pred (S (S (S (S O))))).

   S (S (S O)) : nat
>> Compute (minusTwo (S (S (S (S O))))).

   S (S O) : nat
>> Compute (S (S (S (S O)))).

   S (S (S (S O))) : nat

S는 computation이 아니라는 사실이 좀더 명확하게 보인다. trivial하죠?

Fixpoint

이제 지금까지와는 조금 다른 함수를 정의해보자. n이 짝수인지 확인하려면 어떻게 해야 할까? 아직 곱셈이나 나눗셈은 배우지 않았으므로 다음과 같은 노가다스러운 방법을 떠올릴 수 있다.

1. 0은 짝수이다.
2. 1은 짝수가 아니다.
3. 그 외의 경우, n의 홀짝성은 n-2 의 홀짝성과 같다.

이를 코드로 옮겨보자.

Definition is_even (n : nat) : bool :=
match n with
| O => true
| S O => false
| S (S n') => is_even n'
end.

그런데 이를 실행시키면 “The reference is_even was not found in the current environment.“라는 오류를 볼 수 있다. is_even의 정의에서 다시 is_even을 사용한 게 원인으로 Definition이 단순한 패턴 매칭이기 때문에 등장하는 오류이다. 생각해보면 is_even (S (S (S O)))를 is_even (S O)로 바꾼다고 계산이 끝나는 게 아니므로, 함수를 다시 재귀적(recursive)으로 적용하는 방법을 찾아야 한다. Coq에서는 Fixpoint가 그 역할을 수행한다.

Fixpoint is_even (n : nat) : bool :=
match n with
| O => true
| S O => false
| S (S n') => is_even n'
end.

아래 예시를 보면서 Definition과 Fixpoint의 차이에 대해 감을 잡아보자.

Definition is_odd (n : nat) : bool := negb (is_even n).

둘 이상의 인자를 가지는 함수도 마찬가지로 정의할 수 있다.

Fixpoint plus (n : nat) (m : nat) : nat :=
match n with
| O => m
| S n' => S (plus n' m)
end.

Coq에서는 plus처럼 n과 m이 모두 같은 타입(nat)인 경우 한번에 묶어서 표기가 가능하다.

Fixpoint mult (n m : nat) : nat :=
match n with
| O => O
| S n' => plus m (mult n' m)
end.

이전 글에서 여러 요소를 한번에 매칭시키는 법을 알아봤다 (※ 이전 글의 Tuples 단락 참조). 이 방식 외에도 2개 이상의 변수를 case by case로 나눌 때 match...with을 중첩해 사용할 수 있다. 두 자연수 n, m이 동일한지 판단하는 함수 is_equal을 작성해봤다.

Fixpoint is_equal (n m : nat) : bool :=
match n with
| O => match m with
       | O => true
       | S m' => false
       end
| S n' => match m with
          | O => false
          | S m' => is_equal n' m'
          end
end.

지금까지 작성한 함수들을 Compute를 통해 확인해보자.

>> Compute plus 3 5.

   8 : nat
>> Compute mult 3 5.

   15 : nat
>> Compute is_equal 2 2.

   true : bool
>> Compute is_equal 3 5.

   false : bool

Fixpoint (extra)

CoqIDE를 사용해 실습을 진행했다면 Fixpoint를 사용해 함수를 정의할 때마다 결과창에 눈길을 끄는 문구가 출력됐을 것이다. 아니라면 다시 plus를 예시로 들어보자.

다음 두 함수를 작성하고 나오는 메시지를 확인하자.

Fixpoint plus (n m : nat) : nat :=
match n with
| O => m
| S n' => S (plus n' m)
end.

Fixpoint another_plus (n m : nat) : nat :=
| match m with
| O => n
| S m' => S (another_plus n m')
end.

올바르게 수행했다면 결과창에서 각각 아래와 같은 메시지를 볼 수 있다.

plus is defined
plus is recursively defined (decreasing on 1st argument)

another_plus is defined
another_plus is recursively defined (decreasing on 2nd argument)

앞서 Fixpoint를 이용해 함수를 재귀적으로 정의할 수 있다고 했으므로 xxx is recursively defined 부분은 별로 놀랍지 않다. 그런데 이어진 괄호 안의 문장은 어떤 의미일까?

Coq에서 함수를 정의할 때 가장 중요한 점은 “모든 함수는 언젠가 종료되어야 한다”라는 사실이다. 다시 말해, 무한 루프를 비롯해 끝나지 않을 가능성이 있는 함수의 정의는 원칙적으로 허용되지 않는다. 이를 위해서는 정의된 함수가 항상 유한 시간 내에 끝나는지 판단하는 방법이 있어야 한다.

음? 함수가 유한 시간 내에 계산이 끝나는지를 판단이라고 하면 튜링머신에서 다뤘던 정지 문제(Halting Problem)가 떠오른다. 당황스러운 점은 이건 계산 불가능한 문제로 잘 알려져 있다는 사실이다. 그럼 Coq는 대체 어떻게 하는 걸까.

Coq에서는 항상 종료되는 함수를 보장하기 위해 조금 엄격한 조건을 적용한다. <software foundations>에서는 structural recursion 이라는 말로 이를 설명한다. 즉,

• 함수의 인자에 따른 base case가 존재하고
• 함수의 인자들 중 매 재귀마다 decreasing하는 게 있다면

해당 Fixpoint 정의는 모든 경우에 항상 종료된다고 확신하는 것이다. 이를 벤 다이어그램으로 나타내면 다음과 같다.

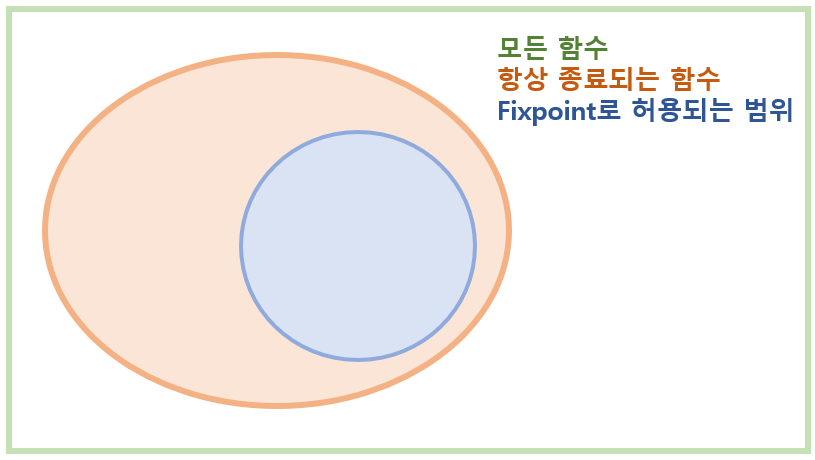
실제로 아래와 같이 정의한 함수 always_zero는 모든 입력에 대해 O를 반환하지만 Coq에서는 오류를 내뱉는다.

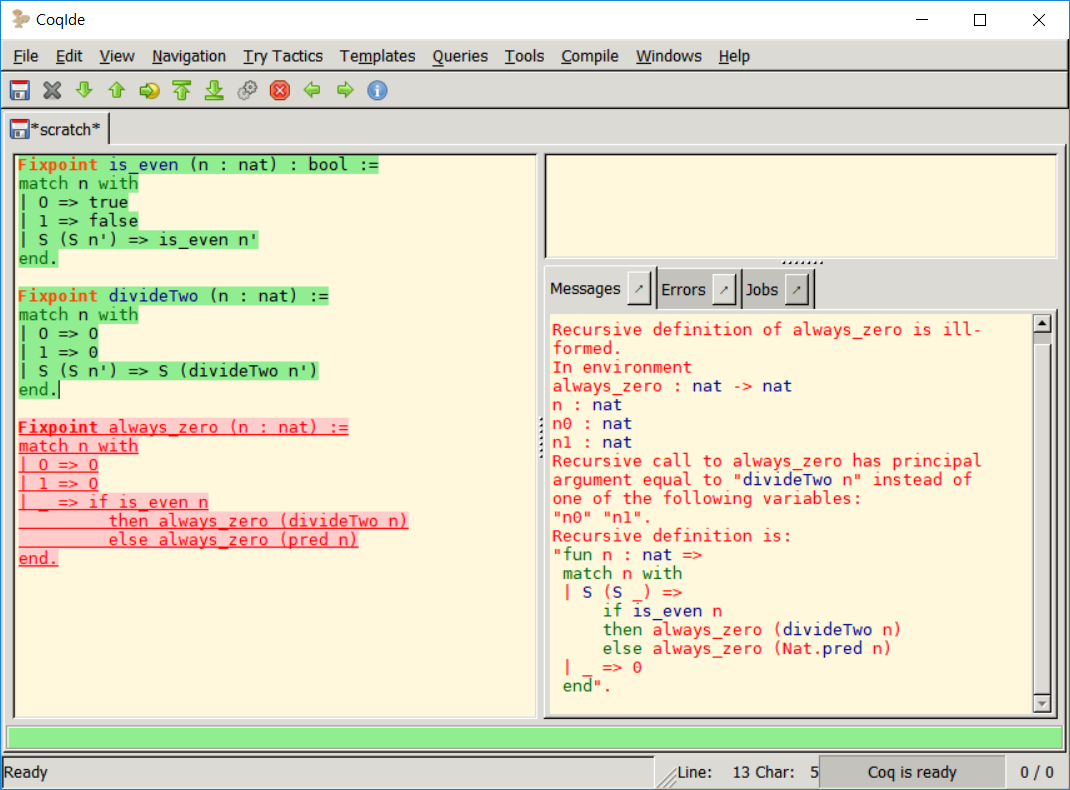
여기서 무한루프의 위험이 있는 계산을 수행할 수 없다와 무한한 요소를 다루는 논리를 펼칠 수 없다 는 다른 의미라는 것을 이해하자. 실제로 계산을 수행하지 않고도 Coq는 충분히 다양한 논리를 표현할 수 있다.