이제 Coq를 이용해 간단한 증명을 직접 작성해보자.

Notation

본론을 시작하기에 앞서 전에 만들었던 plus, mult 에 infix notation을 정의하자.

Notation "x + y" := (plus x y)
                       (at level 50, left associativity)
                       : nat_scope.
Notation "x * y" := (mult x y)
                       (at level 40, left associativity)
                       : nat_scope.

이전에 bool에 대해 x && y 를 정의하던 때보다 뭔가 이것저것 늘어났다. prefix, postfix notation과는 달리 infix notation에서는 모호한(ambiguous) 문장이 생길 수 있다. 일반적으로 (x+y*z)라는 표현식을 쓸 때 우리는 ((x+y)*z)가 아닌 (x+(y*z))를 의도한다. 위 코드에서의 역할을 간단히 요약하면

  • level (0 ~ 100 사이의 정수)
    (x+y)의 level이 50, (x*y)의 level이 40으로, (x+y*z)가 (x+(y*z))로 해석되도록 한다.
  • associativity (left associativity)
    (x+y+z)가 (x+(y+z))가 아닌 ((x+y)+z)로 해석되도록 한다.

가 된다. 사실 여기까지는 Coq에 이미 정의되어 있으므로 굳이 새로 타이핑할 필요는 없다

Proof by simplification

이제 Coq로 수학적 정리를 표현해보자. Coq에서 정리는 다음 형태를 가진다. (Theorem, Lemma, Corollary, Example 모두 동일한 형태인데 이것들이 어떻게 다른지는 아직 잘 모르겠다.)

Theorem (name) : (statement).
Proof.
(tactics)
Qed.

그럼 앞서 정의된(혹은 이미 Coq에 정의되어 있는) nat 타입에 대해 다음 문장을 생각해보자

O은 nat에서 덧셈에 대한 왼쪽 항등원이다. (i.e. \( \forall n:nat, 0+n=n \) )

참고를 위해 plus의 정의를 다시 가져왔다.

Fixpoint plus (n m : nat) :=
match n with
| O => m
| S n' => S (plus n' m)
end.

먼저 증명하고자 하는 명제를 서술하자. 이름은 plus_0_n으로 지었다.

Theorem plus_0_n : forall n:nat, 0 + n = n.

다음으로 증명 시작을 나타내는 Proof.를 쓴다.

Proof.

그럼 (CoqIDE 기준) 오른쪽 위에 subgoal이 나타난 것을 확인할 수 있다.

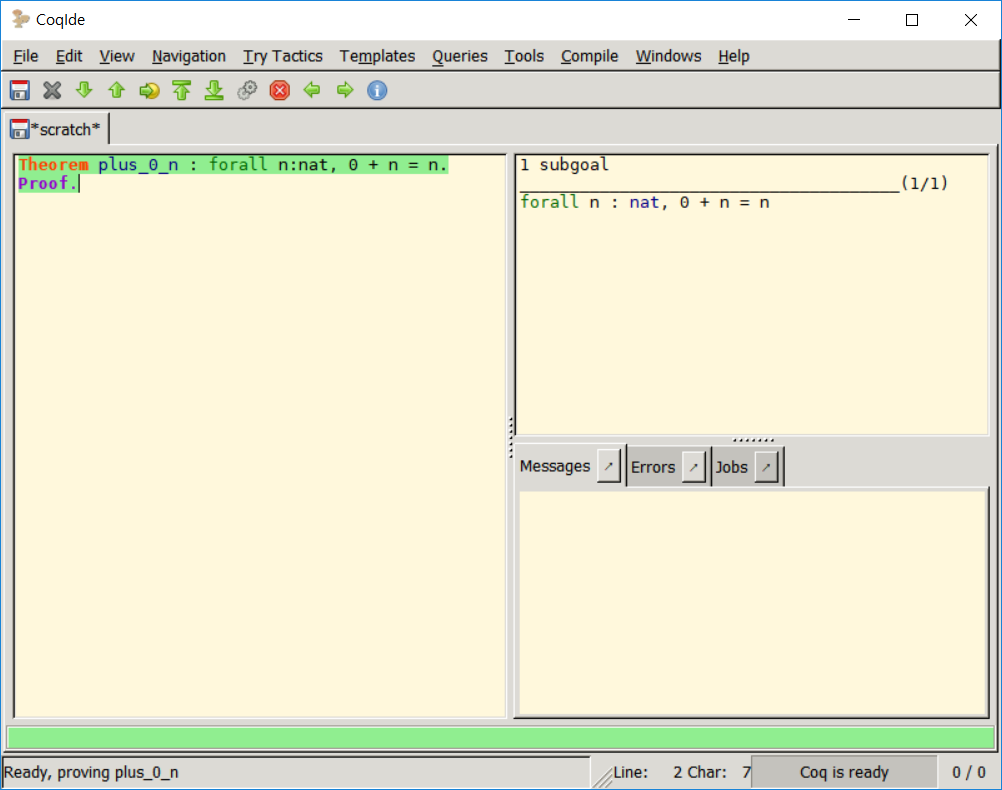
subgoal에서 n 앞에 forall 한정자(quantifier)가 붙어있다. 종이에 펜으로 증명을 시작할 때와 마찬가지로 “어떤 자연수 n에 대해” 를 쓰면서 forall을 떼놓고 생각하자. Coq에서는 intros tactic이 그 역할을 수행한다.

intros n.

subgoal이 어떻게 변했는지 살펴보자. 다음으로 simpl. 을 적용하면 subgoal 창의 메시지는 다음과 같이 변한다.

(simpl. 적용 이전)

1 subgoal
n : nat
______________________________________(1/1)
0 + n = n

(simpl. 적용 이후)

1 subgoal
n : nat
______________________________________(1/1)
n = n

등호 왼쪽이 바뀌었다. Coq에서 0 + n, 다시 말해 plus O n을 인식하고 plus의 정의에 따라 이를 n으로 단순화시킨 것이다. (plus n m에서 n이 O이면 match...with 에 따라 결과는 m이 된다. 이해가 잘 가지 않는다면 plus의 정의를 다시 살펴보자)

마지막으로 이정도는 맞다고 자동으로 넘어가줘도 될거같지만 reflexivity.를 이용하자. 그러면 n=n임이 받아들여지면서 “No more subgoals.” 라는 메시지가 보인다. 이제 Qed.를 통해 증명을 끝낼 수 있다.

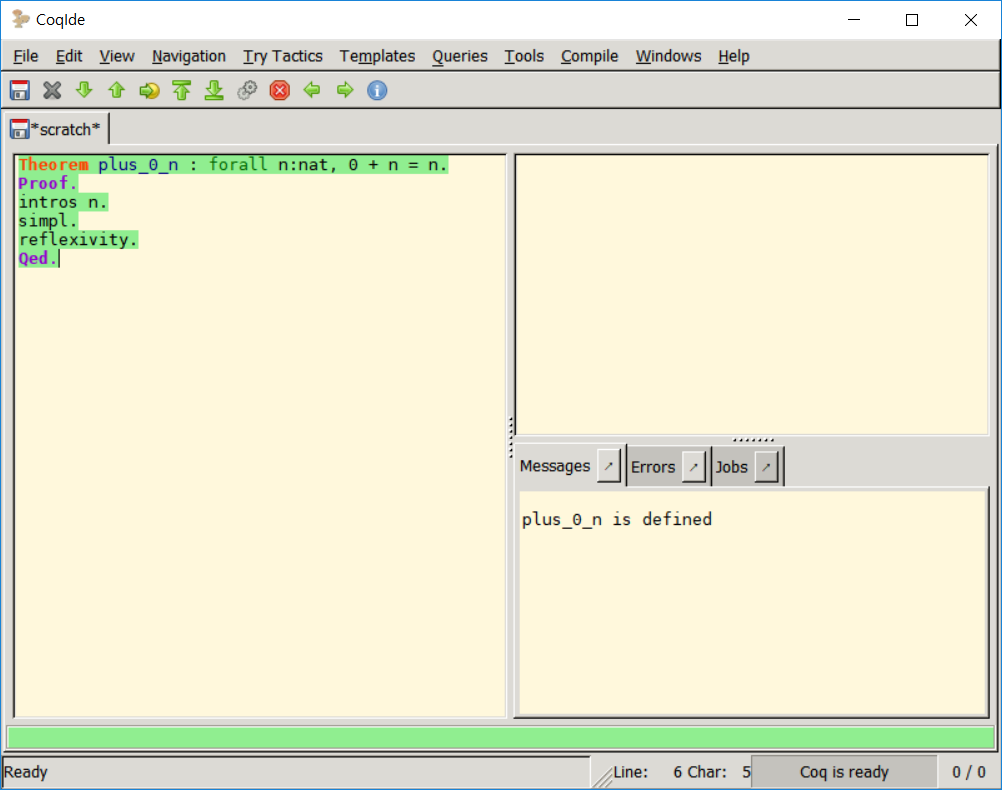
그런데 위 코드에서 simpl.을 지워도 Coq는 정상적으로 동작하고 plus_0_n이 증명되었음을 받아들인다. 사실 reflexivity.는 simpl.과 유사한 방식으로 치환을 수행할 수 있으며, 실제로 simpl.보다 조금 더 넓은 범위를 수행한다. 그런데 왜 굳이 simpl.을 썼을까?

이는 두 tactic의 목적 차이에서 나온다. reflexivity는 주로 a=b 형태의 subgoal을 만족시키는 데 사용하고, 치환/확장을 수행해 양변이 일치하면 subgoal을 달성시킨다. 반면 simpl.은 subgoal 자체를 달성시키려는 기능 없이, 사용자의 이해를 돕는 선까지만 치환/확장을 수행한다고 이해할 수 있다.

Proof by rewriting

이제 다음 정리를 증명해보자.

\(\forall n\,m\,:\,nat,\,n=m\rightarrow n+n=m+m \)

이전에 설명된 내용을 통해 여기까지는 쉽게 작성할 수 있다.

Theorem plus_same : forall n m:nat, n=m -> n+n=m+m.
Proof.
intros n m.

그런데 simpl.을 적용해도 아무런 차이가 나타나지 않는다. 이전의 0+n은 plus의 정의에서 바로 치환이 가능했지만 이번엔 딱히 변화가 없다. 다시 종이와 펜을 들고있다고 상상해보자. \(P \rightarrow Q\) 를 증명할 때 \(P \rightarrow Q\)임을 바로 보이는 것과, 일단 \(P\)를 참이라고 가정하고 \(Q\)가 참임을 보이는 것 중 어느 쪽이 편리할까? 후자의 방법을 사용하기 위해 n = m을 전제조건으로 포함시키자.

intros H.

그러면 subgoal 창은 다음과 같이 변한다.

1 subgoal
n, m : nat
H : n = m
______________________________________(1/1)
n + n = m + m

전제조건 H에서 n=m이라고 했으므로 n을 m으로 바꿔써도 되지 않을까? Coq에서는 이를 수행하는 rewrite tactic이 있다.

rewrite -> H.

이를 적용하면 등호 왼쪽의 n이 m으로 바뀌면서 subgoal이 아래처럼 변한다.

1 subgoal
n, m : nat
H : n = m
______________________________________(1/1)
m + m = m + m

이제 등호를 기준으로 양쪽이 일치하므로 reflexivity.를 이용해 증명을 끝낼 수 있다. Qed.까지 끝났다면 rewrite -> H.를 rewrite <- H.로 바꿔보고 rewrite가 어떤 식으로 동작하는지 감을 잡아보자.