[Coq 입문] Ch02. Proof by tactics (2)

Proof by Case Analysis

다뤄야 하는 대상이 복잡해지면 simpl이나 rewrite만으로는 충분하지 않은 경우가 있다. 잠시 예전 글에서 정의했던 is_equal을 가져오면서 여기에 새로운 Notation을 추가하자.

Fixpoint is_equal (n m : nat) : bool :=
match n with
| O => match m with
       | O => true
       | S m' => false
       end
| S n' => match m with
          | O => false
          | S m' => is_equal n' m'
          end
end.

Notation "x =? y" := (eqb x y) (at level 70) : nat_scope.

이제 거의 비슷하게 생긴 다음 두 명제를 증명해보자.

• \( \forall n : nat, 1+n \neq 0 \)
• \( \forall n : nat, n+1 \neq 0 \)

먼저 1+n은 plus와 notation의 정의로부터 S n으로 simplified될 수 있고, 이를 이용하면 위의 명제는 simpl. 로 증명이 끝난다.

Theorem O_cannot_be_1_n : forall n:nat, (1+n =? 0) = false.
Proof.
intros n.
simpl.
reflexivity.
Qed.

하지만 n+1은 simpl.을 시도해도 아무런 변화가 일어나지 않는다. 그런데 reflexivity.를 적용하(려고 시도하)면 Unable to unify “false” with “n + 1 =? 0” 라는 오류를 볼 수 있다. 1+n과 달리 n+1은 n이 O인지 S n' 형태인지에 따라 결과값이 달라지기 때문에 Coq가 한번에 처리할 수 있는 역량을 벗어난다. 그렇다면 경우를 나누어서 처리하는 방법을 떠올릴 수 있다. destruct tactic이 그 역할을 담당한다.

Theorem O_cannot_be_n_1 : forall n:nat, n+1 =? 0 = false.
intros n.
simpl.
destruct n.

여기까지 적용했다면 각 경우가 나뉘어지면서 2개의 subgoal이 나타난다.

2 subgoals
______________________________________(1/2)
(0 + 1 =? 0) = false
______________________________________(2/2)
(S n + 1 =? 0) = false

이어서 증명을 진행해도 되지만, Coq에서는 각 subgoal에 대한 증명임을 명확히 하기 위해 보조 마크를 사용할 수 있다 (bullet을 이용한 개조식 서술을 생각하면 된다). 이번 경우 각 subgoal은 reflexivity.로 바로 증명이 끝난다.

Theorem O_cannot_be_n_1 : forall n:nat, n+1 =? 0 = false.
intros n.
simpl.
destruct n as [ | n'] eqn:E.
- reflexivity.
- reflexivity.
Qed.

여기서 as [ | n']은 n을 경우에 따라 나누면서 만들어지는 새로운 변수에 이름을 제공하기 위해 사용했다 (O는 새로운 변수가 필요하지 않지만 S xxx 의 경우는 xxx 자리에 사용할 새로운 변수가 필요). as를 사용하지 않아도 Coq에서 자동으로 이름을 제공하지만, 의미를 명확히 하기 위해 가능하면 직접 이름을 제시하는 것이 좋다.

마찬가지로 eqn:E 역시 추가적인 가독성을 제공한다. 조금 전 n을 경우에 따라 나누었지만 그게 n = O인 경우와, n = S n'인 2가지라는 사실을 알기 위해서는 (디테일을 기억하고 있지 않다면) nat의 정의까지 다시 올라가야 한다.destruct tactic을 사용할 때 eqn:(name)을 덧붙이면 각 경우를 가정으로 표기해 현재 다루고 있는 subgoal이 어떤 경우에 해당하는지를 조금 더 친절하게 알려준다. subgoals 창에 나타나는 메시지를 보면 이를 좀더 잘 이해할 수 있다.

1 subgoal
n : nat
E : n = 0
__________________________(1/1)
(0 + 1 =? 0) = false

1 subgoal
n, n' : nat
E : n = S n'
__________________________(1/1)
(S n' + 1 =? 0) = false

나뉘어진 subgoal에 대해 증명을 진행하면서, -를 수행하는 순간 subgoal 창에 나타난 목표가 하나로 한정되는 것을 볼 수 있다. -나 +, *같은 bullet이 일종의 scope 한정자 역할을 하는 셈이다. scope의 활용을 좀더 이해하기 위해 다른 예제를 살펴보자.

Theorem andb_commutative : forall b c, andb b c = andb c b.
Proof.
  intros b c. destruct b. eqn:Eb.
  - destruct c eqn:Ec.
    + reflexivity.
    + reflexivity.
  - destruct c eqn:Ec.
    + reflexivity.
    + reflexivity.
Qed.

중첩이 조금 더 깊게(nested) 이루어지는 상황을 대비해 {, }을 사용해서도 scope 표기가 가능하다.

Theorem andb_commutative' : ∀b c, andb b c = andb c b.
Proof.
  intros b c. destruct b eqn:Eb.
  { destruct c eqn:Ec.
    { reflexivity. }
    { reflexivity. } }
  { destruct c eqn:Ec.
    { reflexivity. }
    { reflexivity. } }
Qed.

Proof by Induction

다음으로 이전에 다뤘던 plus_0_n과 유사하지만 다른 tactic을 사용해야 하는 경우를 알아보자.

Theorem plus_n_0 : forall n:nat, n+0=n.
Proof.
intros n.
(* TODO *)
Qed.

simpl.은 아무런 변화가 없고, destruct n as [|n']을 적용하자 무언가 진척이 있어보인다.

2 subgoals
______________________________________(1/2)
0 + 0 = 0
______________________________________(2/2)
S n' + 0 = S n'

첫 번째는 reflexivity로 간단히 해결 가능하지만 두 번째 subgoal에 simpl.을 적용하면 다음과 같이 변한다.

1 subgoal
n' : nat
______________________________________(1/1)
S (n' + 0) = S n'

뭐지 데자뷰인가 다시 destruct를 적용해 시도해봤지만 같은 패턴이 반복된다.

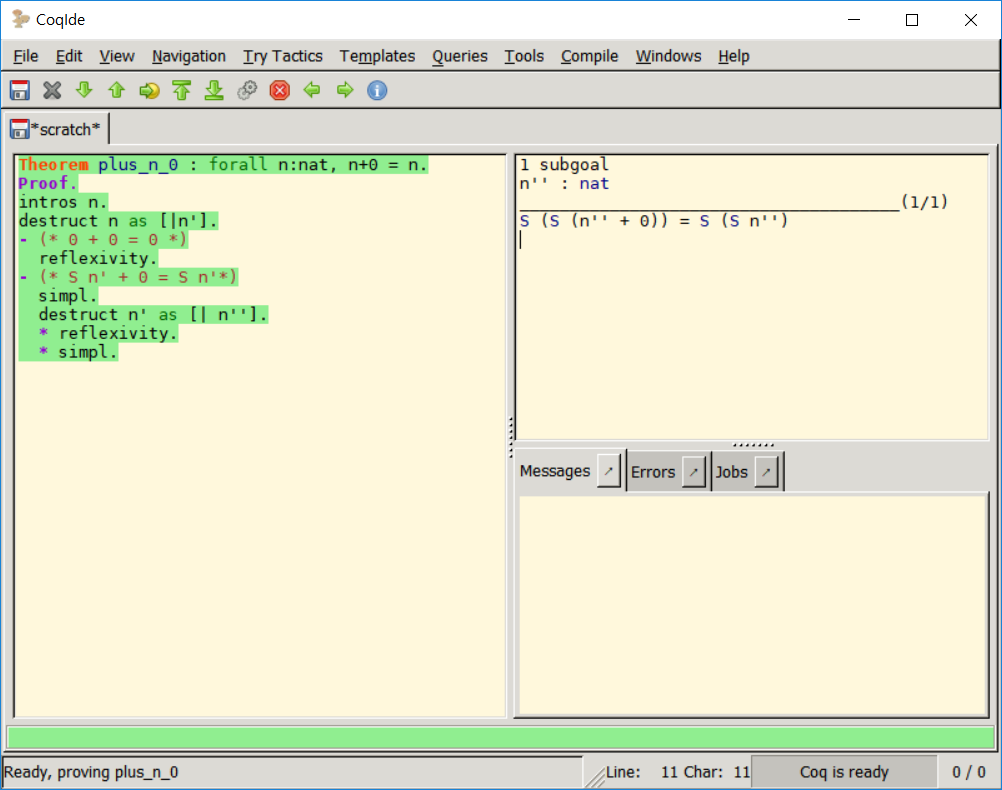
그러면 이 무한한 경우의 수를 모두 하나씩 보여야 할까? 이는 애초에 불가능하다. 그렇다면 어떤 접근을 사용할 수 있을까.

\( \forall P(-)((P(0)\land \forall n (P(n) \implies P(n+1))) \implies \forall n P(n)) \)

다루고자 하는 대상이 자연수(nat)이므로 수학적 귀납법을 생각해볼 수 있다. 위 수식에 나타나 있듯이 자연수에 대한 성질 \(P(n)\)에 대해,

• \(P(0)\)이 성립하고
• \(\forall n, P(n) \implies P(n+1)\) 이면

모든 자연수 n에 대해 P(n)이 성립, 다시 말해 \(\forall n, P(n)\) 이 된다.

이전 destruct때와 유사하게induction tactic을 적용하면 2개의 subgoal이 나타난다. 여기서 n'은 destruct때와 마찬가지 의미를, IH는 Induction Hypothesis에 IH라는 이름을 붙였음을 뜻한다.

induction n as [|n' IH].

첫 번째 subgoal(0+0=0)을 reflexivity로 끝내고 2번째 subgoal인 induction step에 집중하자. 이때 앞서 이름붙인 IH를 사용할 수 있다.

1 subgoal
n' : nat
IH : n' + 0 = n'
______________________________________(1/1)
S n' + 0 = S n'

simpl.을 적용하면 goal은 S (n' + 0) = S n'으로 변하고, 여기에 rewrite IH를 적용하면 증명을 끝낼 수 있다. 전체 코드는 아래와 같다.

Theorem plus_n_0 : forall n:nat, n+0 = n.
Proof.
intros n.
induction n as [|n' IH].
- (* 0 + 0 = 0 *)
  reflexivity.
- (* S n' + 0 = S n' *)
  simpl.
  rewrite -> IH.
  reflexivity.
Qed.

Proofs within Proofs

앞서 Induction Step을 보일 때 중간에 전제조건으로 주어진 IH를 이용해 손쉽게(?) 증명을 마쳤다. 이처럼 증명 도중에 사용할 수 있는 정리들이 있다면 간결함과 가독성을 높이는 데 큰 도움이 된다. 바깥에서 정의된 Lemma나 Corollary 등을 사용할 수도 있지만, 그러기엔 사소한 경우 assert를 이용해 증명 도중에 작은 보조정리들을 추가할 수 있다.

Theorem mult_0_plus
 : forall n m : nat, (0 + n) * m = n * m.
Proof.
  intros n m.
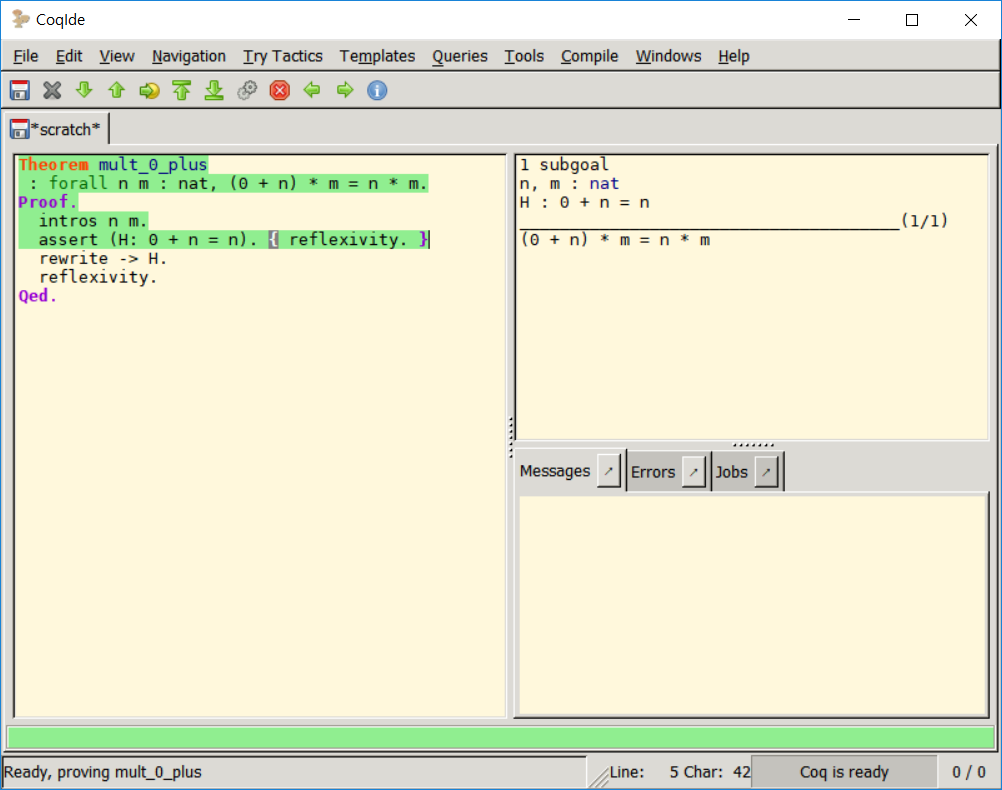
  assert (H: 0 + n = n).

assert 를 추가하면 2개의 subgoal이 나타난다. 첫 번째는 assert로 추가된 명제, 두 번째는 원래 목표였던 subgoal이다. assert로 추가한 내용을 증명하고 나면 induction에서와 마찬가지로 이를 이용할 수 있다.

지금까지 Coq의 기초적인 tactic들에 대해 알아보았다.