[Coq 입문] Ch03. Working with Structured Data (2)
by nyan101
Reasoning About Lists
리스트에 대한 간단한 정리를 증명해보자.
Theorem nil_app : forall l:natlist, [] ++ l = l.
Proof.
reflexivity.
Qed.
대상이 natlist라는 점만 제외하면 이전의 forall n:nat, 0+n=n과 같은 형태이다. nat에서와 마찬가지로 natlist도 destruct를 통해 생성규칙에 따라 경우를 나눌 수 있다.
Theorem tl_length_pred :
forall l:natlist, pred (length l) = length (tl l).
Proof.
intros l.
destruct l as [| n l'] eqn:E.
- (* l = [] *)
reflexivity.
- (* l = n::l' *)
reflexivity.
마찬가지로 수학적 귀납법(induction tactic) 역시 적용 가능하다. nat에서의 귀납법과 마찬가지로 base step과 induction step으로 이루어져 있으며, 각각
- base step :
l = []인 경우, nat에서n = 0인 경우에 해당한다. - induction step :
l = n :: l'인 경우, nat에서n = S n'인 경우에 해당한다.
이때 n::l', 다시 말해 cons n l'은 2개의 인자를 받는다는 점에 유의하자. 예시를 통해 natlist에서의 induction이 어떻게 이루어지는지 살펴보자.
Theorem app_assoc :
forall (l1 l2 l3 : natlist), (l1 ++ l2) ++ l3 = l1 ++ (l2 ++ l3).
Proof.
intros l1 l2 l3.
induction l1 as [| n l1' IH1].
- (* l1 = [] *)
reflexivity.
- (* l1 = n :: l1' *)
simpl.
rewrite -> IH1.
reflexivity.
Qed.
nat에서와 거의 동일한 방식으로 증명이 끝났다. 그러면 이제 그렇지 않은 경우를 통해 Coq를 어떤 식으로 사용하는지 감을 잡아보자.
이전 글에서 natlist를 뒤집어주는 rev함수를 정의했다. 편의를 위해 아래에 코드를 다시 가져왔다.
Fixpoint rev (l : natlist) : natlist :=
match l with
| nil => nil
| h::t => rev t ++ [h]
end.
증명하고자 하는 정리(성질)는 다음과 같다.
\( \forall l:natlist,\,\mathrm{length}\,(\mathrm{rev}\,l) = \mathrm{length}\,l \)
그런데 지금까지 배운 것들을 이용해 증명을 시도하면 도중에 막히는 부분을 마주하게 된다.
Theorem rev_length : forall l:natlist, length (rev l) = length l.
Proof.
intros l.
induction l as [| n l' IH].
- (* l = [] *)
reflexivity.
- (* l = n::l' *)
simpl.
rewrite <- IH.
Abort.
이 시점의 subgoal을 살펴보자.
1 subgoal
n : nat
l' : natlist
IH : length (rev l') = length l'
______________________________________(1/1)
length (rev l' ++ [n]) = S (length (rev l'))
이 subgoal을 해결하기 위해서는 length 와 ++ 연산(app) 사이의 연관관계를 이용할 수 있어야 한다. 그런데 현재로서는 이에 대해 별다른 유의미한 성질을 가지고 있지 않다. 그렇다면 유의미한 성질을 찾아 증명을 추가하자.
직관적으로 다음 성질을 생각해 볼 수 있다. 증명은 induction을 이용하면 비교적 간단하다.
Theorem app_length :
forall (l1 l2 : natlist), length (l1 ++ l2) = (length l1) + (length l2).
Proof.
intros l1 l2.
induction l1 as [| n l1' IH].
- (* l1 = [] *)
reflexivity.
- (* l1 = n::l1' *)
simpl.
rewrite -> IH.
reflexivity.
Qed.
이제 이 성질을 이용해 rev_length를 다시 증명해보자.
Theorem rev_length :
forall l : natlist, length (rev l) = length l.
Proof.
intros l. induction l as [| n l' IH1].
- (* l = [] *)
reflexivity.
- (* l = n::l' *)
simpl. rewrite -> app_length, plus_comm.
simpl. rewrite -> IH1. reflexivity.
Qed.
먼저 app_length 를 사용해 앞서 막혔던 subgoal인 length (rev l’ ++ [n]) = S (length (rev l’)) 을 length (rev l’) + length [n] = S (length (rev l’)) 로 바꿀 수 있고, length [n]은 1이므로 subgoal은 다시 length (rev l’) + 1 = S (length (rev l’))이 된다. 이제 nat에서의 +연산은 교환법칙을 만족한다는 사실(plus_comm)과 induction hypothesis를 이용하면 나머지는 쉽게 증명할 수 있다.
Search
그런데 app_length나 plus_comm의 경우 지난 글들에서 증명해본 정리들이기 때문에 어렵지 않게 내용을 다시 떠올리고 증명에 이용할 수 있다. 그렇다면 작성한 지 오래되었거나 다른 사람이 만들어 둔 라이브러리를 가져온다면 그 안에 있는 내용들을 전부 알고 있어야 할까? 그래서는 의미가 없다. Coq에서는 Search를 통해 사용할 수 있는 정리들에 대한 검색을 지원한다. 이해를 돕기 위해 plus 를 검색해봤다.
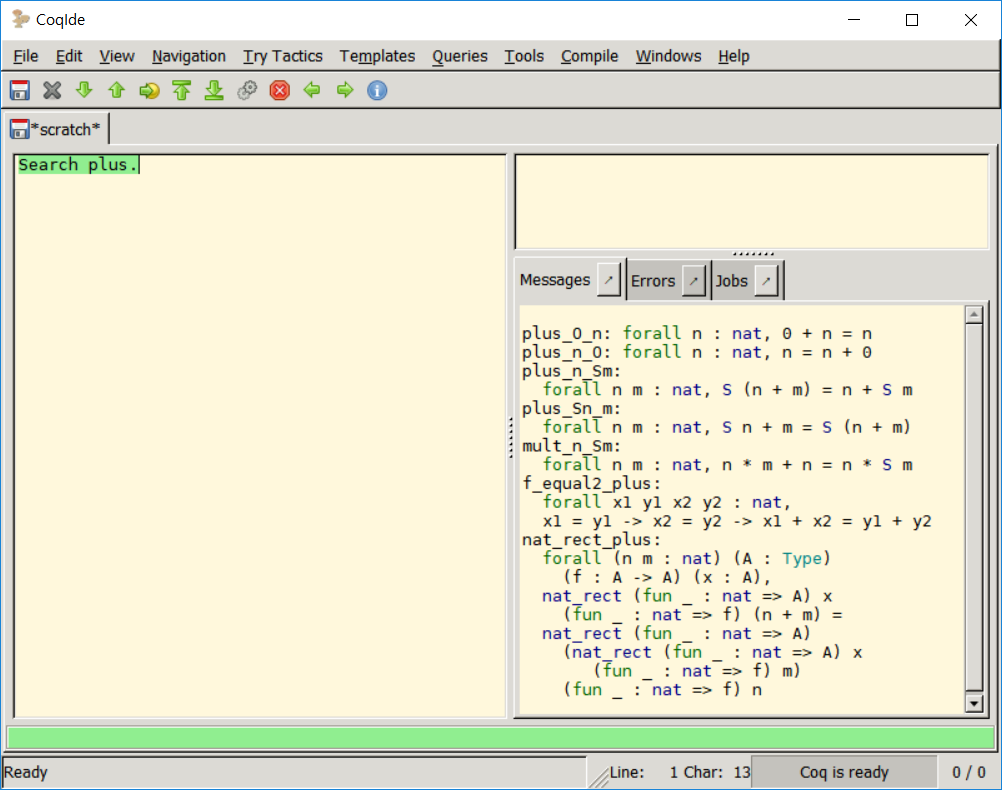
오른쪽 아래에서 검색 결과를 확인할 수 있다.
Options
잠시 natlist의 기본적인 함수인 head(hd)와 함께, 리스트의 n번째 원소를 가져오는 get_nth 를 작성해보자. 이때 ‘n번째’는 0-based index를 의미한다.
Definition hd (l:natlist) : nat :=
match l with
| nil => O
| h::t => h
end.
Fixpoint get_nth (l:natlist) (n:nat) : nat :=
match l with
| nil => O
| h::t => match n with
| O => h
| S n' => get_nth t n'
end
end.
위 두 함수는 같은 문제점을 가진다. 아래 경우를 생각해 보자.
>> Compute get_nth [1;4;2;0;3;5] 3.
0 : nat
>> Compute get_nth [1;4;2] 5.
0 : nat
값이 존재하지 않는 경우 기본값으로 0을 반환하도록 설정했기 때문에, “정말 해당 자리에 0이 있는 경우”와 “값이 존재하지 않는 경우”를 구분하지 못한다. 0이 아닌 다른 어떤 값을 기본값으로 정해도 비슷한 문제가 발생한다. 이 문제를 해결하기 위해 단순히 nat의 정의에 Null을 추가하는 방법을 떠올려볼 수 있다.
Inductive nullable_nat : Type :=
| NULL
| O
| S (n : nat).
0과 Null을 구분할 수 있지만 어딘가 석연치 않다. 군더더기가 붙은 느낌은 둘째치고 S (S NULL) 을 비롯해 의도하지 않은 nat 요소들이 만들어질 수 있다는 새로운 문제가 생겼다. 그렇다면 어떻게 해야 할까? 다음과 같이 nat을 한 차례 포장하는 방법을 생각해보자.
Inductive natoption : Type :=
| None
| Some (n : nat).
그러면 get_nth는 natoption을 사용해 다시 쓸 수 있다.
Fixpoint get_nth (l:natlist) (n:nat) : natoption :=
match l with
| nil => None
| h::t => match n with
| O => Some h
| S n' => get_nth t n'
end
end.
이제 Some h(의미를 가진 nat 반환값)와 None(의미를 가지지 않는 디폴트값)이 명확히 구분된다. 그런데 상황에 따라 무의미한 경우에 None 대신 기본값을 사용하더라도 natoption이 아닌 nat이 필요한 순간이 올 수 있다. 아래에 작성한 option_elim을 통해 주어진 natoptoin 인자가 유의미한 값인 경우 해당하는 nat으로, None인 경우 디폴트 값(d : nat)으로 변환할 수 있다.
Definition option_elim (d : nat) (o : natoption) : nat :=
match o with
| Some n => n
| None => d
end.
이렇게 option을 이용한 방식은 비단 nat뿐만이 아니라 다른 어떤 타입에도 적용시켜 ‘유의미한 값’과 ‘무의미한 값’을 구분할 수 있다. 이는 하스켈에서 Maybe monad가 동작하는 방식과 정확히 일치한다. 하스켈에서는 이를 다음과 같이 설명하고 있다.
The
Maybedatatype provides a way to make a safety wrapper around partial functions, that is, functions which can fail to work for a range of arguments. For example,headandtailonly work with non-empty lists. Another typical case, which we will explore in this section, are mathematical functions likesqrtandlog; (as far as real numbers are concerned) these are only defined for non-negative arguments. (원문)
모나드가 무엇인지, 어떻게 응용할 수 있는지에 대한 자세한 설명은 이번 글에서 다루는 범위를 벗어난다. 열정적인 독자(만약 있다면)를 위해 유투브 Computerphile 채널에서 모나드에 대해 간략히 설명한 영상을 첨부한다.
Subscribe via RSS
