[Coq 입문] Ch04. Polymorphism & Higher-Order Functions (2)

High-Order Functions

다른 함수를 다룰 수 있는 함수를 고차 함수(higher-order function)라고 한다.

Definition do3times {X:Type} (f:X->X) (a:X) : X := f (f (f a)).

>> Check @do3times

   : @do3times : forall X : Type, (X -> X) -> X -> X

이 do3times는 함수 f와 인자 a를 받아 a에 f를 3번 적용한 결과를 돌려준다. 함수를 인자로 제공한다는게 어떤 의미인지 살펴보자

>> Definition doubleMe (n:nat) : nat := n+n.
>> Compute do3times doubleMe 3.

   : 24 : nat

Filter

이제 좀더 유용한 고차 함수들에 대해 알아보자. filter는 X타입의 리스트(list X)와 원소 X에 대한 판정함수(predicate, \(f:X\rightarrow bool\))를 받아 주어진 predicate를 만족하는(i.e. true를 리턴하는) 원소들만을 남긴다.

Fixpoint filter {X:Type} (test:X->bool) (l:list X) : (list X) :=
match l with
| [] => []
| h::t => if test h then h::(filter test t)
                    else (filter test t)
end.

>> Compute filter evenb [1;2;3;4;5;6].

   : [2; 4; 6] : list nat

조금 더 복잡한 predicate에서도 마찬가지로 잘 동작한다.

Definition length_is_1 {X : Type} (l : list X) : bool :=
  (length l) =? 1.

 >> filter length_is_1 [ [1; 2]; [3]; [4]; [5;6;7]; []; [8] ]
 
    : [ [3]; [4]; [8] ] : list (list nat).

filter를 이용하면 다양한 함수를 쉽게 작성할 수 있다. nat으로 이루어진 리스트에서 짝수의 개수를 세는 함수를 생각해보자. 고차 함수를 사용하지 않는다면 아래처럼 작성될 것이다.

Fixpoint count_even (l : list nat) : nat :=
match l with
| [] => O
| h::t => if evenb h then (count_even t) + 1
                     else (count_even t)
end.

그런데 filter를 이용하면 동일한 내용을 다음과 같이 간결한 형태로 작성할 수 있다.

Definition count_even' (l:list nat) : nat := length (filter evenb l).

Compute를 통해 확인해보자

>> Compute count_even [1;2;3;4;5;6].

   : 3 : nat
>> Compute count_even' [1;2;3;4;5;6].

   : 3 : nat

Anonymous Functions

앞서 filter를 테스트할 때 length_is_1이라는 함수를 작성했다. 그런데 이렇게 한번 쓰고 말 함수를 위해 따로 정의를 작성하고 이름을 붙이는 건 조금 낭비라는 생각이 든다. 이렇게 단순한 내용이면 즉석에서 바로 만들어서 사용해도 되지 않을까? 다른 많은 함수형 언어들과 마찬가지로 Coq도 람다식(lambda expression)을 지원한다.

>> Compute do3times (fun n => n*n) 2.

   : 256 : nat

위 코드에서 (fun n => n*n)은 “n을 받아 n*n을 반환하는 함수”를 의미한다. 이를 이용하면 앞서 작성한 length_is_1예제를 다음과 같이 다시 쓸 수 있다.

>> filter (fun l => (length l) =? 1) [ [1; 2]; [3]; [4]; [5;6;7]; []; [8] ].

   : [ [3]; [4]; [8] ] : list (list nat)

Map

filter만큼 유용하게 사용되는 함수로 map이 있다. map은 함수 f와 리스트 l( = [a1;a2;…;an])을 받아 [f a1; f a2; … ; f an]을 반환한다.

Fixpoint map {X Y : Type} (f:X->Y) (l:list X) : (list Y) :=
match l with
| [] => []
| h::t => (f h)::(map f t)
end.

예시를 통해 map이 어떻게 동작하는지 알아보자.

>> Compute map (fun n=>n*n) [1;2;3;4;5].

   : [1; 4; 9; 16; 25] : list nat

map의 정의에서 타입을 X, Y 로 따로 정의했으므로 결과 리스트의 타입이 입력 리스트의 타입과 같을 필요는 없다.

>> Compute map evenb [1;2;3;4;5].

   : [false; true; false; true; false] : list bool

Fold

filter, map과 함께 함수형 언어의 삼신기(…)로 불리는 마지막 함수 fold에 대해 알아보자. 일부 언어(ex:파이썬)에서는 reduce라는 이름으로 제공된다. ~~파이썬 2에서는 기본제공이었는데 파3에서는 functools 라이브러리로 따로 빠짐~~

Fixpoint fold {X Y : Type} (f:X->Y->Y) (l:list X) (b:Y) : Y :=
match l with
| nil => b
| h::t => f h (fold f t b)
end.

정의만 봐서는 아직 어떤 함수인지 잘 감이 오지 않는다. 결론부터 말하면 fold는 인자 2개를 받는 함수 f, 리스트를 받아 각 인자들에 함수 f를 누적하면서 적용해 최종 결과를 반환하는 함수라고 할 수 있다.

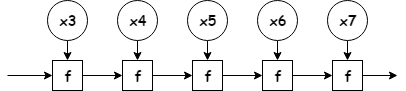
fold 함수의 구조

위 그림을 보면 “f를 리스트의 인자에 누적해서 적용한다”라는 말을 이해할 수 있다. 그런데 그림을 보면 시작점, 다시 말해 f에 맨 처음 제공될 인자가 하나 필요하다. 이를 위해 fold 함수를 정의할 때 함수 f와 리스트 l 외에도 시작점 역할을 수행할 인자(b)를 함께 명시했음에 유의하자.

예제를 통해 fold에 대해 감을 잡아보자.

>> Compute fold plus [1;2;3;4] 0.

   : 10 : nat.
>> Compute fold mult [1;2;3;4] 1.

   : 24 : nat.
>> Compute fold andb [true;true;false;true] true.

   : false : bool
>> fold app [[1];[];[2;3];[4]] [].

   : [1;2;3;4] : list nat.

Functions that Construct Functions

지금까지 소개한 고차 함수는 모두 “함수를 인자로 받는” 경우였다. 이제 함수를 반환하는 함수에 대해 알아보자. 다음 함수는 x를 받아 “nat타입 인자를 받아 상수 x를 반환하는 함수”를 반환한다.

Definition constfun {X:Type} (x:X) : nat->X := fun (n:nat) => x.

constfun을 이용해 어떤 입력에도 무조건 true를 반환하는 fun_true 함수를 만들어보자.

>> Definition fun_true := constfun true.
>> Compute fun_true 123.

   : true : bool

결과 함수를 따로 저장하지 않고도 사용할 수 있다.

>> Compute (constfun 5) 999.

   : 5 : nat

사실 이런 생소한 함수가 아니더라도 지금까지 다뤘던 많은 함수들이 함수를 결과로 반환한다. 엄밀히 말해, 모든 다인자 함수(둘 이상의 인자를 받는 함수)들은 함수를 반환하는 일인자 함수(하나의 인자를 받는 함수)라고 말할 수 있다. 단순하게 plus를 생각해보자.

>> Check plus.

   : nat -> nat -> nat

지금까지 nat->nat->nat은 “nat인자 2개를 받아 nat을 반환하는 함수”라고 해석해왔다. 그런데 ->는 타입들 사이에서 정의된 right associative한 binary operator이다. 이를 고려하면서 위 타입을 다시 엄밀히 표기하면 nat->(nat->nat) 가 된다. 따라서 다음과 같은 논리를 펼 수 있다.

nat->nat는 “nat을 받아 nat을 반환하는 함수” 타입이다.
nat->(nat->nat)은 nat을 받아 <nat을 받아 nat을 반환하는 함수>를 반환하는 함수 타입이다.

예제를 통해 위 말이 가지는 의미를 알아보자. plus에 nat 인자를 ‘하나만’ 제공했다.

>> Definition plus3 := plus 3.
>> Check plus3.

   : plus3 : nat->nat

이렇게 정의한 plus3은 nat->nat 타입을 가진다. 구체적으로 어떤 함수인지 살펴보자.

>> Compute plus3 5.

   : 8 : nat
>> Compute plus3 10.

   : 13 : nat
>> do3times plus3 2.

   : 11 : nat
>> do3times (plus 10) 7.

   : 37 : nat

plus3은 입력으로 들어오는 인자에 3을 더해주는 함수임을 어렵지 않게 확인할 수 있다. 이렇게 plus3을 만드는 과정이나 마지막의 (plus 10) 처럼 인자의 일부만 제공된 적용시켜 함수를 만들 수 있으며, 이를 함수에 대한 partial application이라고 한다.

지금까지 함수형 프로그래밍 언어로서의 Coq에 대해 알아보았다. 다음 장에서는 다시 Coq의 여러 tactic들에 대해 다룬다.