[ML] Knockoff Net: 랜덤한 입력으로 다른 모델을 모방할 수 있을까?
by nyan101
발상: Knockoff Nets
어제(2일) 대학원에서 Mario Fritz 박사님의 AI Security에 대한 강연을 들어볼 수 있었다. 딥러닝이 대세가 되면서 등장한 여러 보안 문제들에 대한 특강이었는데, 그중 Model Stealing(구체적으로는 Functionality Stealing)에 대해 다룬 knockoff-net 관련 내용이 흥미로워 pytorch로 구현해보았다. 다만 노트북이라는 한계로 원본 논문보다는 디테일을 다소 단순화했다(…)
Knockoff net을 간단히 말하면 이미 학습이 끝난 모델 V를 블랙박스로 이용해 (V와 같은 기능을 하도록) 자신의 모델 A를 학습시키는 것이라고 할 수 있다. 모델을 학습시킬 때 마주하는 문제 중 하나는 소위 좋은 학습 데이터를 구하기 어렵다는 점이다. Classification 문제를 생각해봐도 대표적인 MNIST나 CIFAR-10 등 유명한 일부를 제외하면 잘 정제되어 있고 + 올바른 라벨이 붙어있는 데이터는 구하기 쉽지 않다. 이때 이런 고급 데이터셋으로 학습된 모델 V를 이용해 (해당 데이터셋 없이) 새로운 모델 A를 학습시킨다고 생각해 보자.
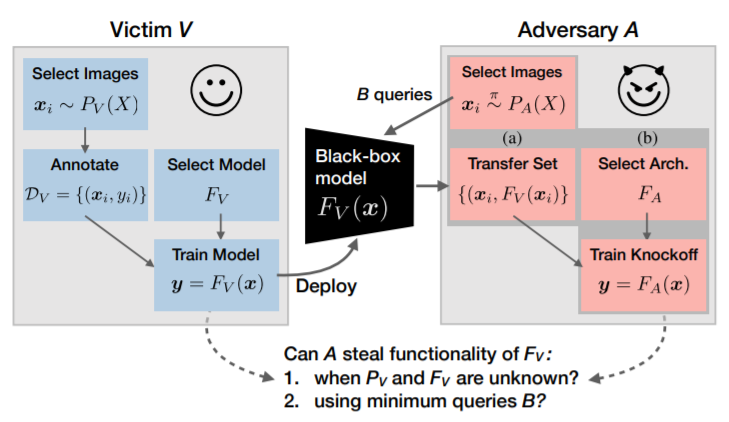
핵심은 모델 V를 블랙박스처럼 사용해 모델 A를 위한 학습 데이터셋을 생성하는 것이다. 딥러닝의 원리를 생각해보면 이를 좀더 직관적으로 이해할 수 있다. Classification Model의 경우
- 가상의 함수 \(F_{ideal}\) : 이미지를 넣으면 원하는 라벨이 one-hot 인코딩되어서 나오는 함수
- 모델 V의
.forward()(이하 \(F_V\)) : 위 \(F_{ideal}\)을 모방하는 함수
라고 하면 \(F_V = F_{ideal}\)가 우리가 원하는 결과이며, 이를 위해 모델 V의 파라미터를 조절하는 것이다. 다시 말해, 딥러닝 모델의 학습은 주어진 Training Dataset \(D=\{ (d_{sample}, d_{label}) \} \)에 대해 \(F_{V}(d_{sample}) \simeq F_{ideal}(d_{sample})=d_{label}\) 이면 일반화된 다른 입력에 대해서도 \(F_{V}(sample) \simeq F_{ideal}(sample)=label\) 이 될 것이라는 기대에 기반한다.
그렇다면 \(D\)가 아닌 다른 데이터셋 \(R=\{ (r_{sample}, \_) \} \)에 대해 \(F_A(r_{sample}) \simeq F_V(r_{sample})\)이 되도록 조정한다면, 일반화된 샘플에 대해서 \(F_{A}(sample) \simeq F_{V}(sample) \simeq F_{ideal}(sample)\)이 되지 않을까? knockoff net 논문에서는 그림이라는 선은 지켰지만1 본 블로그에서는 랜덤한 노이즈를 통해 \(R\)을 생성했다.
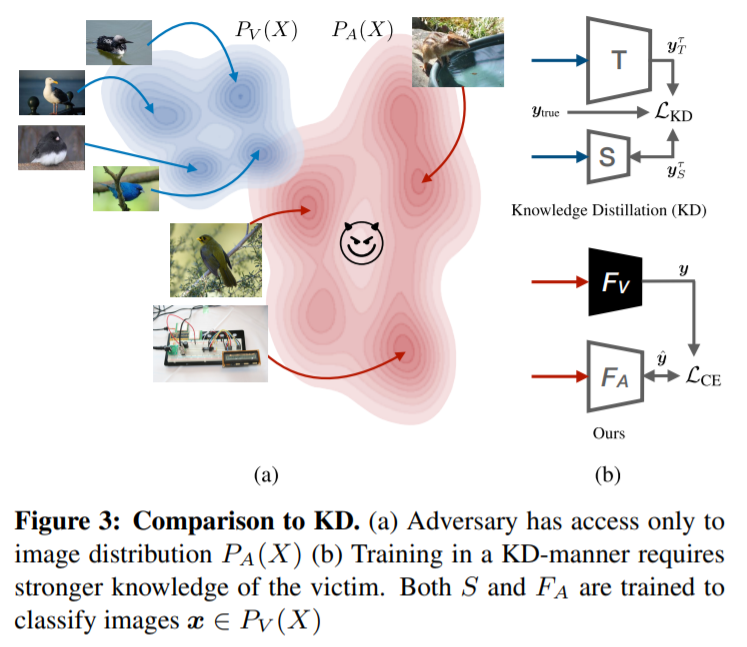
(그림 출처: Knockoff Nets: Stealing Functionality of Black-Box Models )
제대로 학습된 모델 V 만들기
먼저 모델 V를 만들기 위해 이전 글에서 MNIST 분류기를 가져왔다. 출력값 확인을 위해 기존 모델의 끝에 softmax 레이어를 추가해 출력벡터의 각 요소를 0~1 사이로 조절했다. 이 net은 MNIST를 정상적으로 학습한 모델이 된다.
class MyModel(nn.Module):
def __init__(self):
super(MyModel, self).__init__()
self.layer1_conv = nn.Conv2d(1, 6, 5, 1) # 입력 1개, 출력 6개, 필터 크기는 5x5, 1칸 단위로 이동하면서 필터를 씌운다
self.layer1_relu = nn.ReLU() # 활성화 함수. ReLU(x) 는 max(x, 0)과 같다
self.layer1_pool = nn.MaxPool2d(2) # 각 2x2 칸마다 최대값 하나씩만을 남긴다
self.layer2_conv = nn.Conv2d(6, 16, 5, 1)
self.layer2_relu = nn.ReLU()
self.layer2_pool = nn.MaxPool2d(2)
self.fc = nn.Linear(16*4*4, 10)
self.softmax = nn.Softmax(dim=1)
def forward(self, x):
x1 = self.layer1_conv(x) # 1x28x28 형식의 데이터가 6x24x24 형식으로 변환된다
x2 = self.layer1_relu(x1) #
x3 = self.layer1_pool(x2) # 6x24x24 형식의 데이터가 6x12x12 형식으로 변환된다
x4 = self.layer2_conv(x3) # 6x12x12 형식의 데이터가 16x8x8 형식으로 변환된다
x5 = self.layer2_relu(x4) #
x6 = self.layer2_pool(x5) # 16x8x8 형식의 데이터가 16x4x4 형식으로 변환된다
x7 = x6.view(-1, 256) # 16x4x4 형식의 데이터가 256-벡터로 변환된다
x8 = self.fc(x7) # 256-벡터가 10-벡터로 변환된다
x9 = self.softmax(x8) # 최종 10-벡터의 각 값은 0~1 사이 값을 가지고 총합은 1이 된다
return x9
net = MyModel()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(net.parameters())
위 모델을 학습시키면 5 epoch 후 test set에 대해 97.82%의 정확도를 얻을 수 있다. 적어도 내 노트북에선 그렇게 나왔다
랜덤 노이즈 입력에서 모델 V 따라하기
모델 A를 위해 랜덤한 데이터를 생성해보자. MNIST가 28x28 크기의 흑백 이미지이므로 torch.randn 함수를 사용해 같은 크기의 이미지를 만들었다.

이 이미지를 앞서 학습이 끝난 모델 V (net) 에 입력하면 아래와 같은 출력을 내놓는다.
tensor([2.6900e-10, 4.2002e-23, 6.6886e-01, 1.5307e-04, 1.0798e-23, 4.9928e-07,
3.4142e-08, 1.7324e-13, 3.3099e-01, 4.0419e-12])
모델에 따르면 이 이미지는 66.9%로 숫자 2, 33.1%로 숫자 8인 모양이다 물론 이 결과는 별다른 의미를 가지지 않는다. 그렇다면 이렇게 만든 (랜덤한 이미지, 예측값)을 학습 데이터로 사용해 모델 A를 학습시키면 어떻게 될까?
net_koff = MyModel() # 기존 net과 구조는 동일하다.
criterion_koff = nn.BCELoss() # 라벨이 아닌 두 '분포'에 대한 학습이므로 BCELoss 사용
optimizer_koff = optim.Adam(net_koff.parameters())
num_epoch = 10
st = time.time()
print(f"training with {len(train_data)} noises...")
for epoch in range(num_epoch):
tot_loss = 0
for x,y in train_loader:
noise_x = torch.randn_like(x) # train data와 동일한 크기의 랜덤 데이터를 생성
y_target = net(noise_x).detach() # 모델 V(net)의 예측값을 타겟으로 설정
y_pred = net_koff(noise_x) # 모델 A(net_koff)의 예측 y_pred가 y_target이 되도록 학습
loss = criterion_koff(y_pred, y_target)
tot_loss += loss
optimizer_koff.zero_grad()
loss.backward()
optimizer_koff.step()
print(f" - Epoch {epoch+1}/{num_epoch}. loss: {tot_loss}....(elapsed {time.time() - st}s)")
print(f"done (elapsed {time.time() - st}s)")
# 실제 MNIST의 test data로 test accuracy 측정
net_koff.eval()
acc, tot = 0, 0
for x, y in test_loader:
y_pred = net_koff(x)
acc += (y==y_pred.argmax(1)).sum()
tot += len(y)
print(f"test accuracy of knockoff net: {acc}/{tot} ({100*acc/tot}%)")
일반적인 학습과 거의 동일하지만 train_loader에서 가져온 데이터 대신 torch.randn_like()를 이용해 같은 크기의 노이즈로 대체했다. 또한 라벨 y를 사용하는 대신 net의 출력값을 y_target으로 지정했음에 유의하자. 말이 안 되는 것 같지만 놀랍게도 학습이 끝난 후 net_koff의 test accuracy를 측정해보면 83.6% 라는 높은 수치를 보여준다.
내부 구조가 달라도 일단 따라해보기
아마 net과 net_koff의 내부 구조(Conv 레이어 크기, hidden layer개수 등)가 동일하다는 점 때문에 학습 결과 내부 파라미터들이 높은 확률로 서로 비슷한 값을 가졌기 때문이라고 생각할 수 있다. 그래서 원본 모델(net)과 내부 구조부터 다르게 한 MyAnotherModel 클래스를 새로 작성했다.
class MyAnotherModel(nn.Module):
def __init__(self):
super(MyAnotherModel, self).__init__()
self.layer1_conv = nn.Conv2d(1, 8, 5, 1)
self.layer1_relu = nn.ReLU()
self.layer1_pool = nn.MaxPool2d(2)
self.layer2_conv = nn.Conv2d(8, 12, 5, 1)
self.layer2_relu = nn.ReLU()
self.layer2_pool = nn.MaxPool2d(2)
self.fc1 = nn.Linear(12*4*4, 50)
self.fc_relu = nn.ReLU()
self.fc2 = nn.Linear(50, 10)
self.softmax = nn.Softmax(dim=1)
def forward(self, x):
x1 = self.layer1_conv(x) # 1x28x28 형식의 데이터가 8x24x24 형식으로 변환된다
x2 = self.layer1_relu(x1) #
x3 = self.layer1_pool(x2) # 8x24x24 형식의 데이터가 8x12x12 형식으로 변환된다
x4 = self.layer2_conv(x3) # 8x12x12 형식의 데이터가 12x8x8 형식으로 변환된다
x5 = self.layer2_relu(x4) #
x6 = self.layer2_pool(x5) # 12x8x8 형식의 데이터가 12x4x4 형식으로 변환된다
x7 = x6.view(-1, 192) # 12x4x4 형식의 데이터가 192-벡터로 변환된다
x8 = self.fc1(x7) # 192-벡터가 50-벡터로 변환된다
x9 = self.fc_relu(x8)
x10 = self.fc2(x9) # 50-벡터가 10-벡터로 변환된다
x11 = self.softmax(x10)
return x11
학습은 이전 MyModel의 net_koff와 동일한 방법으로 이루어졌다. 실험 결과 이렇게 만든 net_koff2는 MNIST test set에서 약 56.3%라는 정확도를 보였다. 일반적인 MNIST에서 이는 크게 의미있는 수치가 아니지만2 학습에 사용한 입력이 전부 torch.randn([1, 28, 28])이라는 점을 고려하면 꽤 놀라운 결과라고 할 수 있다.
UPD: 몇번 더 돌려보니 70, 80%를 넘어 MyAnotherModel에서도 91% 이상을 찍는 경우도 발생한다. 랜덤시드에 따른 문제같은데, 불필요한 오해를 피하기 위해 블로그 본문에서는 여러 번의 테스트 중 낮은 수치를 소개했다.
후기(?)
<파이널 판타지 14>라는 갓겜이 있다. 파티를 맺고 던전을 돌면서 보스를 잡는 게임인데, 직업별로 최적화된 “딜사이클”이라는 개념이 존재한다. 실력이 미숙해 딜미터기 최하위를 차지하던 시절, 네임드 유저분이 올린 사이클을 그대로 따라하니 원리는 모르겠지만 어쨌든 딜이 오르는 경험을 한 적이 있다. 그땐 원리 이해도 못하고 무작정 따라하는게 본 실력이라고 할 수 있나 싶었는데 knockoff net이 학습되는 과정을 보면 그런 생각은 잠시 접어둬도 될 것 같다(…)
p.s. 실험에 사용한 전체 코드는 여기에서 볼 수 있다. (PC 전용)
Subscribe via RSS
