[PyTorch] 01. PyTorch의 기본 구조
by nyan101
요새는 뭘 찾아봐도 딥러닝이 나온다..
성향이 continuous, gradient 같은 거랑은 안 맞아서 최대한 피해보려고 했지만 결국 시대의 흐름에 거스르지 못하고 어떻게 사용하는지 정도는 알아두는게 좋을 것 같아서 정리해봤다.
요구사항(prerequisite)
- python에 대한 기초지식
(ex:ABC.xyz()는 클래스/객체ABC안에 있는xyz라는 함수를 호출하는 것이다) - 함수에 대한 개념(규칙에 따라 input → output으로 이어지는 블랙박스로 이해해도 된다)
- 머릿속 이미지화를 위한 약간의 상상력(?)
tensor 클래스
tensor는 \(n_1 \times n_2 \times \cdots \times n_d \) 개의 숫자를 \(d\)차원으로 정렬한 객체이다. 편의상 예시는 2차원 이하만을 다룰 예정이지만 임의의 차원을 가질 수 있다는 점은 알아두자.
생성
x = torch.tensor([[1,2,3],[4,5,6]]) # 1~6으로 채워진 2차원 텐서(크기 2x3)를 생성
y = torch.rand((3, 4)) # 0~1 사이의 임의의 수로 채워진 2차원 텐서(크기 3x4)를 생성
z = torch.zeros((1,2,3)) # 0으로 채워진 3차원 텐서(크기 1x2x3)를 생성. 1로 채우는 ones()도 있다
x.shape # 텐서 x의 크기. 위 예시에서는 torch.Size([2, 3])
연산
numpy에서와 비슷하게 다양한 연산을 지원한다. 왠지 있을법한건 대충 다 있다고 보면 된다.
z = x.mean() # x의 모든 원소들의 평균
z = x.sum() # x의 모든 원소들의 합
z = x + y # x,y의 각 원소들에 대한 element-wise 덧셈. + 대신 *를 쓰면 곱셈 연산이 된다
# 예외적으로 y가 스칼라이거나 1x1 크기인 경우 x의 모든 원소에 대해 연산이 이루어진다
z = x @ y # x,y의 행렬곱. x,y가 크기 제약조건(N x M 행렬과 M x R 행렬)을 만족해야 한다
# 예외적으로 y가 1차원인 경우 상황에 맞는 행벡터or열벡터인 것처럼 처리된다
함수명이 _로 끝나는 경우는 in-place 연산을 의미한다.
x.add_(3) # x에 3을 더한다
x.sub_(4) # x에 4를 뺀다
x.zero_() # x를 0으로 만든다
tensor와 autograd
딥러닝은 결국 gradient descent 과정이다. 이를 이해하기 위해 gradient란 무엇이고, 어떻게 구할 수 있는지 알아보자.
연산 그래프(Computational Graph)
먼저 텐서들의 연산에 대한 머리속 구조(Mental Model)를 살짝 바꾸는 작업이 필요하다.
x = torch.tensor([3])
y = torch.tensor([4])
z = x + y
흔히 이런 코드를 보면 x와 y를 3, 4가 들어있는 일종의 상자로 생각하고, z를 7이 저장된 새로운 상자로 이미지하곤 한다(아래 그림의 왼쪽). int나 float 같은 primitive 타입에서는 이렇게 생각해도 문제가 없지만 tensor라는 ‘객체’는 조금 다르게 동작한다.
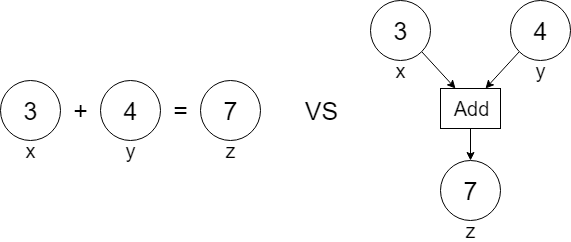
왼쪽 그림에서와 달리 오른쪽에서 z는 연산의 결과값(7)뿐만이 아닌, 어떻게 그 값을 얻게 되었는지를 역추적할 수 있는 링크를 볼 수 있다.1 이렇게 얻은 z를 이용해 연산을 진행할수록 그림의 그래프도 마찬가지로 확장해나갈 수 있는데, 이러한 형태의 그래프를 연산 그래프(Computational Graph)라고 한다.
연산 그래프를 만들기 위해서는 torch.tensor를 정의할 때 requires_grad=True를 설정해야 한다. 대부분의 경우 선언 시점에 requires_grad를 설정하겠지만, 코드 중간에 이를 변경해야 하는 경우 .requires_grad_() 함수에 True/False를 넘김으로써 온/오프가 가능하다.
x = torch.tensor([3.0], requires_grad=True) # tensor([3.], requires_grad=True)
y = torch.tensor([4.0], requires_grad=True) # tensor([4.], requires_grad=True)
z = x + y # tensor([7.], grad_fn=<AddBackward>)
y.requires_grad_(False) # 이제 y는 연산 그래프에서 gradient를 계산하지 않음
그래디언트 계산
그럼 이제 다음과 같은 질문이 떠오른다.
- “required_grad에서 grad는 무엇을 의미하는가”
- “이렇게 연산 그래프를 만들어서 무엇을 얻는가”
먼저 첫 질문에 답해보자. 그래디언트(gradient, 이하 grad)는 간단히 말해 각 변수가 ‘현재 시점’에서 목적함수를 변화시키는 정도라고 할 수 있다. 예로 \(y = -x^4 + 10x^3 + 10x^2 - 15x - 4\)의 식에서 \(y\)를 목적함수라고 하면 아래와 같은 그래프를 얻는다.
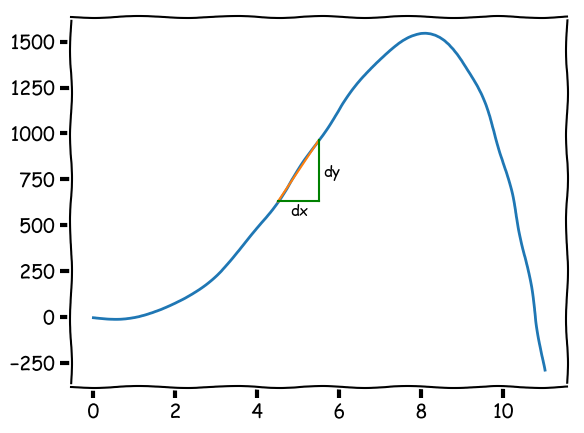
그래프에서 \(x=5\)인 순간에 x의 그래디언트2 \(\frac{\partial y}{\partial x}\)는 335이며, 이는 \(x=5\) 근처에서 x가 \(d\) 만큼 변하면 y는 \(335d\) 만큼 변하게 됨을 의미한다. 다변수 함수 \(y=f(x_1,x_2)\)에 대해서도 마찬가지로 \(\frac{\partial y}{\partial x_1}, \frac{\partial y}{\partial x_2}\) 를 구할 수 있다.
이제 연산 그래프의 진가가 드러난다. 연산 그래프를 통해 최종 결과물(=목적함수)이 어떻게 계산된 것인지 역추적할 수 있으므로, 이를 처음 시작까지 거슬러 올라가면 각 입력 변수들이 목적함수에 얼마나 영향을 끼치는지를 구할 수 있다. 이 모든 과정은 최종 결과물(=y)에서 .backward() 함수 호출을 통해 이루어진다.
x = torch.tensor([5.0], requires_grad=True)
y = -1*(x**4) + 10*(x**3) + 10*(x**2) - 15*x - 4
y.backward() # dy/dx가 계산된다
print(x.grad) # tensor([335.])
조금 더 복잡한 연산의 경우에도 마찬가지 작업이 가능하다.
x1 = torch.tensor([1.0], requires_grad=True)
x2 = torch.tensor([2.0], requires_grad=True)
x3 = torch.tensor([3.0], requires_grad=True)
y = x1*x2*x3*x3 + 7*x1*x2 - x2*x2 - 4*x1*x3
y.backward() # y를 계산하는데 연관된 모든 x들에 대해 dy/dx가 계산된다
print(x1.grad) # tensor([20.])
print(x2.grad) # tensor([12.])
print(x3.grad) # tensor([8.])
grad와 머신러닝
grad가 왜 중요할까? .backward() 와 grad를 이용해 선형 회귀 문제를 풀어보자.3
xs = torch.tensor([1.0, 2.0, 3.0, 4.0, 5.0, 6.0]) # fitting하고자 하는 데이터
ys = torch.tensor([3.0, 6.5, 5.0, 6.0, 8.0, 12.0]) #
# y = a*x + b 형태의 선형 함수로 근사한다
a = torch.tensor([0.0], requires_grad=True) # a의 초기값은 0
b = torch.tensor([7.0], requires_grad=True) # b의 초기값은 7
y_pred = a*xs + b # a, b를 이용해 y의 예측값을 계산한다
err = ((ys - y_pred)**2).mean() # 예측한 값의 제곱 평균 오차(Mean Square Error)를 구한다
아무 조작도 하지 않은 초기상태(\(a=0, b=7\))에서의 근사는 오른쪽과 같은 모습이다.

이제 err.backward()를 실행하면 무슨 일이 벌어지는지 살펴보자.
err.backward()
print(a.grad) # tensor([-6.6667]). a가 d만큼 변하면 err는 -6.6667*d만큼 변한다
print(b.grad) # tensor([0.5000]). b가 d만큼 변하면 err는 0.5000*d만큼 변한다.
우리는 근사의 오차(=err)가 0에 최대한 가깝게 변하기를 원한다. 그런데 err은 제곱수(양수)이므로 0이 되기 위해서는 - 방향으로 움직여야 하고, 따라서 a는 + 방향으로, b는 - 방향으로 조정하는 것이 좋다는 결론을 내릴 수 있다. 그렇다면 a,b 각각을 ‘얼마나 큰 크기로’ 조정해야 할까? 조정을 위한 기본 원칙을 세워보자.
- (그래디언트는 현재 값 근처에서만 유효하므로) 한번에 너무 많이 움직이면 안 된다
- 목표 함수에 핵심적인 역할을 하는 변수는 그렇지 않은 변수보다 큰 폭으로 변화시키는게 좋다
이만하면 나름 그럴듯한 기준이다. 이를 고려하면 아래와 같은 간단한 변환을 생각할 수 있다.
a -= 0.01 * a.grad # 기술적인 이유로 실제 코드에서는 a.data.sub_(0.01 * a.grad) 이 된다.
b -= 0.01 * b.grad # 기술적인 이유로 실제 코드에서는 b.data.sub_(0.01 * b.grad) 이 된다.
식을 살펴보면 목표 함수(err)가 항상 양수이고, 이를 0에 최대한 가깝게 만드는 것이 목표일 때 위 연산은 항상 올바른 방향으로 변수를 조정한다는 것을 알 수 있다. 이제 이렇게 조정된 a,b를 가지고 다시 앞선 과정을 반복하자. 반복 작업의 편의를 위해 이를 코드로 정리했다.
for i in range(num_adjust):
y_pred = a*xs + b
err = ((y_pred - ys)**2).mean()
err.backward()
a.data.sub_(0.01 * a.grad)
b.data.sub_(0.01 * b.grad)
a.grad.zero_() # 조정이 끝나면 다시 grad값을 0으로 초기화한다
b.grad.zero_() # 이렇게 갱신과 별도로 초기화하는 이유는 추후 다른 글을 통해 설명한다
그렇다면 num_adjust가 증가할수록 실제로 err이 줄어들까? 아래 그림은 조정 횟수에 따른 최종 \(y=ax+b\) 그래프를 정리한 결과이다. 조정 횟수가 증가함에 따라 점차 근사가 정확해지는(=오차가 줄어드는) 것을 확인할 수 있다.
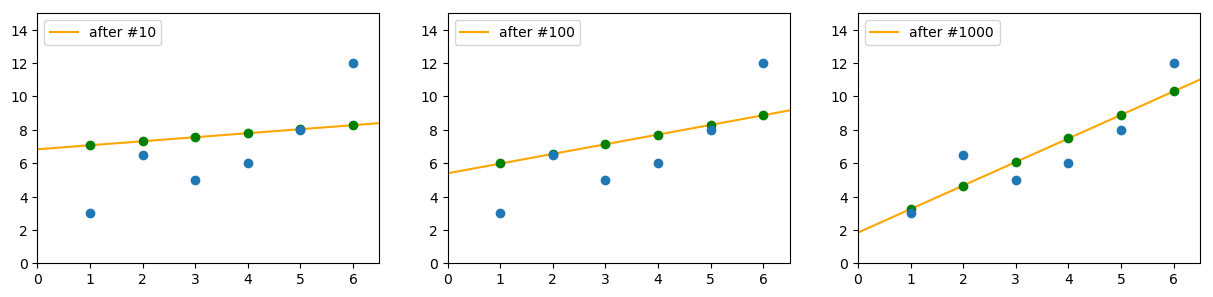
모든 머신러닝은 입력 x에 대해 모델의 출력 y_pred가 참값 y와 가까워지도록(=오차 err이 감소하도록) 만드는 과정임을 생각하면, 앞서 수행한 조정은 단순히 선형 회귀가 아닌 좀더 복잡한 모델에도 마찬가지로 적용 가능하다는 사실을 알 수 있다.
다음 글에서는 pytorch에서 복잡한 모델을 생성하는 방법과, 모델의 여러 파라미터를 좀더 영리하게 조정하는 방법에 대해 알아본다.
-
직관적인 그림을 위해 설명을 단순화했다. 실제로는 모든 텐서가 아닌
requires_grad=True로 설정된 텐서들만이 그래프의 유의미한 노드가 된다. ↩ -
정확한 표현은 ‘x의 편미분값’ 이다. 수학에서 그래디언트는 단일 변수가 아닌, 관여한 전체 변수들에 대한 편미분들의 모음이다. (ex: 다변수 함수 \(y=f(x_1,x_2)\)에서 \(\mathrm{grad}\,y = ( \frac{\partial y}{\partial x_1}, \frac{\partial y}{\partial x_2} )\)) ↩
-
사실 1차원 선형 회귀 문제는 굳이 이런 번거로운 방법을 쓰지 않고도 수학적으로 최적의 답을 구할 수 있다. ↩
Subscribe via RSS
