[PyTorch] 02. nn.Module로 모델 클래스 만들기
by nyan101
학습의 각 단계를 추상화하기
앞서 그래디언트를 이용해 간단한 학습이 이루어지는 과정을 알아보았다. 이전 글의 마지막 코드를 다시 살펴보면 학습의 한 round를 크게 다음과 같은 단계들로 추상화시킬 수 있다.
for i in range(num_adjust):
# 1) 파라미터를 이용해 입력(xs)으로부터 예상 결과를 생성
y_pred = a*xs + b
# 2) 예상 결과(y_pred)와 실제 결과(ys)를 비교해 오차를 계산
err = ((y_pred - ys)**2).mean()
# 3) .backward()를 통해 각 파라미터가 오차에 관여하는 정도를 역산
err.backward()
# 4) 역산된 grad를 바탕으로 파라미터 수정
a.data.sub_(0.01 * a.grad)
b.data.sub_(0.01 * b.grad)
# 5) 파라미터들의 grad값을 0으로 초기화
a.grad.zero_()
b.grad.zero_()
그런데 이번과 같이 모델이 \(y=ax+b\) 처럼 간단한 형태인 경우 파라미터(a, b)들을 각자 관리할 수 있지만, 복잡한 모델의 경우 이는 상당히 번거로운 과정이 될 수 있다. 흩어진 파라미터들을 통합해 관리한다면 어떤 형태가 가능할지 생각해 보자.
params = "통합된 파라미터들을 저장할 모음. list,dict,class,... 중 뭐가 좋을까?"
def init_params(params):
params = "어떤 파라미터를 사용할 것인지 정의하고, 각 파라미터에 초기값 설정"
pass
def predict(x, params):
y_pred = "입력(=x)과 params으로부터 예측값 계산"
return y_pred
def calculate_err(y_pred, y):
err = "예측값(y_pred)과 실제값(y)간의 차이를 계산"
return err
def update_params(params):
"grad를 바탕으로 params를 조절한다"
pass
def clear_grad(params):
"params의 grad 값들을 전부 0으로 초기화한다"
pass
# 추상화된 학습과정
init_params()
for i in range(num_adjust):
# 1) 파라미터를 이용해 입력(xs)으로부터 예상 결과를 생성
y_pred = predict(xs, params)
# 2) 예상 결과(y_pred)와 실제 결과(ys)를 비교해 오차를 계산
err = calculate_err(y_pres, ys)
# 3) .backward()를 통해 각 파라미터가 오차에 관여하는 정도를 역산
err.backward()
# 4) 역산된 grad를 바탕으로 파라미터 수정
update_params(params)
# 5) 파라미터들의 grad값을 0으로 초기화
clear_grad(params)
대부분의 경우 학습과정은 이 형태를 크게 벗어나지 않을 것이다. 그런데 여기서 일부 함수들이 순수 함수(pure function)가 아닌, 내부 상태를 변화시키는 ‘동작’ 을 하는 프로시저(procedure)라는 사실이 눈에 들어온다. 일관성 있는 관리를 위해 각 단계들을 다시 역할에 따라 모아 클래스로 만들 수 있다.
- 예측값 계산 담당
init_params(),predict()
- 오차 계산 담당
calculate_err()
- 파라미터 조정 담당
update_params(),clear_grad()
pytorch 모델은 기본적으로 이러한 분류를 따라 설계된다. 각각은 흔히 model(혹은 module), criterion, optimizer라는 이름으로 불리며, 이들 용어는 특별한 언급이 없는 한 이 블로그에서도 동일한 의미로 약속하자.
Model 클래스 만들기
pytorch 모델 클래스를 위한 기본 틀은 다음과 같다. 선형 함수는 너무 간단하니 3개의 파라미터(a, b, c)를 설정해 2차함수 근사를 위한 모델을 만들었다.
import torch
import torch.nn as nn
class MyModel(nn.Module): # nn.Module 클래스의 확장이 된다
def __init__(self):
# 부모 생성자 호출
super(MyModel, self).__init__()
# 파라미터들의 타입이 torch.tensor가 아니라 nn.Parameter임에 유의
self.a = nn.Parameter(torch.tensor([1.]))
self.b = nn.Parameter(torch.tensor([2.]))
self.c = nn.Parameter(torch.tensor([3.]))
def forward(self, x):
y = self.a * (x**2)
y += self.b * (x**1)
y += self.c
return y
이렇게 정의된 모델 클래스는 다음과 같이 사용할 수 있다.
# fitting 대상 데이터
xs = [ 1.00, 2.00, 3.00, 4.00, 5.00, 6.00, 7.00, 8.00, 9.00 ]
ys = [ 9.15, 5.64, -0.21, -2.36, -0.91, -0.67, 2.65, 10.36, 17.13 ]
# 모델 객체 생성
model = MyModel()
# model.parameters()로 모델의 파라미터에 접근할 수 있다
# 파라미터들의 이름을 같이 보고싶다면 model.named_parameters()를 사용하자
for param in model.parameters():
print(param)
y_pred = model(xs) # model.forward(xs)와 동일
처음 예측을 진행해보면 y_pred 는 (당연하게도) 전혀 들어맞지 않는 결과가 나온다.
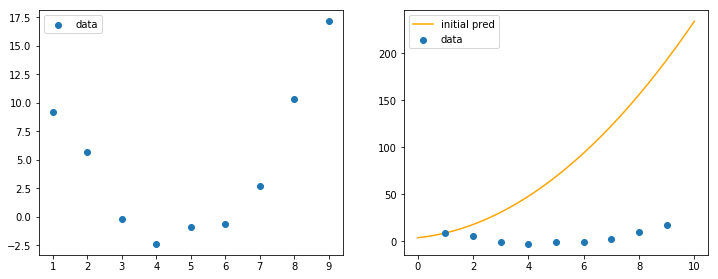
이제 오차를 계산하고 파라미터를 조정해야 한다.
오차 계산하기
이전까지는 오차를 Mean Square Error(MSE)로 정의해 이를 코드상에서 계산했다. 그런데 꼭 이것만이 유일한 답일까? 오차를 정의하는 다른 방법들은 없을까?
잘 알려진 MSE 외에도 Cross Entropy나 KL-divergence와 같은 다양한 방법들이 존재하며, 이들 대부분은 pytorch내부에 이미 구현되어 있다. 이번에는 torch.nn.MSELoss에 정의된 MSE를 그대로 사용하자. 설정할 수 있는 옵션들이 궁금한 사람을 위해 공식 문서가 준비되어 있다.
criterion = nn.MSELoss() # 처음 한 번만 정의
----------
loss = criterion(y_pred, ys) # 매 라운드(epoch)마다. *앞으로는 err 대신 loss라는 용어를 사용한다
loss.backward()
파라미터 조정하기
loss.backward()까지 진행하면 각 파라미터들마다 계산된 .grad를 얻는다. 이제 이를 바탕으로 파라미터를 조정하자. 이전에는 아래와 같은 방식을 이용했다.
self.a -= 0.01 * self.a.grad
self.b -= 0.01 * self.b.grad
self.c -= 0.01 * self.c.grad
...
요약하면 모든 파라미터에 param -= (small_ratio) * param.grad 를 적용하는 것이라고 할 수 있다. 이런 방식을 Stochastic Gradient Descent(SGD)라고 하며, 이밖에도 Adam, ASGD, Rprop 등 다양한 업데이트 방식이 존재한다. 당연하게도 이런 업데이트 알고리즘 역시 pytorch의 torch.optim 내에 구현되어 있다. 여기서는 SGD를 그대로 사용하자. 업데이트 시 변화량에 곱해지는 ‘작은 수’를 lr(learning ratio)이라고 지칭한다.
import torch.optim as optim
optimzer = optim.SGD(model.parameters(), lr=1e-4) # 정의 시점에 model.parameters()를 넘겨준다
----------
loss.backward()
optim.step() # 파라미터 업데이트
optim.zero_grad() # 파라미터들의 grad를 0으로 초기화
All-in-One
이제 전체 코드를 종합해보자.
# Model 클래스 구조
class MyModel(nn.Module):
def __init__(self):
super(MyModel, self).__init__()
self.a = nn.Parameter(torch.tensor([1.]))
self.b = nn.Parameter(torch.tensor([2.]))
self.c = nn.Parameter(torch.tensor([3.]))
def forward(self, x):
y = self.a * (x**2)
y += self.b * (x**1)
y += self.c
return y
# fitting 대상 데이터
xs = torch.tensor([ 1.00, 2.00, 3.00, 4.00, 5.00, 6.00, 7.00, 8.00, 9.00 ])
ys = torch.tensor([ 9.15, 5.64, -0.21, -2.36, -0.91, -0.67, 2.65, 10.36, 17.13 ])
# model과 criterion, optimizer 선언
model = MyModel()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-4)
# 학습
for epoch in range(100000):
y_pred = model(xs)
loss = criterion(y_pred, ys)
optimizer.zero_grad() # .zero_grad()의 위치는 이곳과 .step() 이후 중 어느 곳이든 상관 없음
loss.backward() # 인터넷의 다른 예제들과의 통일성을 위해 loss.backward() 이전에 놓았다
optimizer.step()
if(epoch % 10000):
print(f"Loss after {epoch} steps: {loss}")
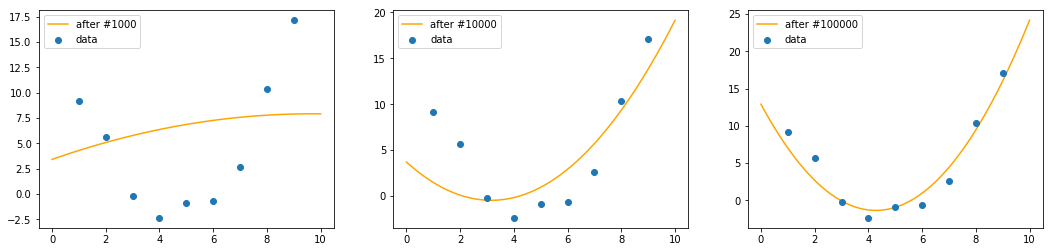
학습 epoch이 증가함에 따라 점차 fitting하고자 하는 데이터에 가까워지는 것을 확인할 수 있다.
Subscribe via RSS
