이번 SCTF(Samsung CTF)의 700점짜리 문제로 튜링머신 설계가 나왔다. 총 4개의 문제 중 3개는 일반적인 오토마타 교과서에서 다루는 언어들(ex: \(L=\{ 0^n1^n | n \geq 0 \}\))이었지만 마지막 단계인 \(L=\{0^p | p \, \mathrm{\,is\,prime}\}\)가 다소 많은 시간을 잡아먹었다. 사실상 소수 판별을 하는 튜링 머신을 설계하라는 문제였는데, 기억상 다른 교재들에서도 이에 대한 명확한 실례는 나와있지 않아 따로 정리했다. 아래 등장하는 그래프의 화살표에서 A/B . P는 “현재 state에서 알파벳 A를 읽었을 때, 테이프에 B를 쓰고 P방향(L, 또는 R)으로 이동한다”라는 의미를 가진다. 이제 필요한 서브루틴을 하나씩 구성해 보자.

step 1. \(L_1 = \{1^n\#0^m\ | n은\,m의\,약수\}\)

먼저 이런 언어를 인식할 수 있는 루틴을 생각해보자. 튜링머신의 테이프를 기준으로 생각하면 다음과 같은 로직을 떠올릴 수 있다.

  1. 가장 왼쪽의 1을 2로 바꾼다
  2. 가장 오른쪽의 0을 3으로 바꾼다
  3. 모든 0이 3으로 바뀌었는지 확인한다(=마지막으로 바꾼 3의 왼쪽이 #인지 확인)
  4. (case 1. 모든 0이 3으로 바뀐 경우) 모든 1이 2로 바뀌었는지 확인한다. → 모두 바뀌었으면 n은 m의 약수, 아직 1이 남아있으면 n은 m의 약수가 아님
  5. (case 2. 아직 0이 남아있는 경우) 더 지울 수 있는 1이 남아있는지 확인한다. → 아직 남아있으면 1. 로, 1이 모두 2로 바뀌어있으면 2들을 모두 1로 바꾼 후 1. 로 돌아간다.

다시 말해, 위 과정은 결국

  • 1과 0을 하나씩 쌍으로 지워가면서
  • 1이 먼저 다 떨어지면 n개의 1을 다시 리필하고
  • 둘이 동시에 떨어진 경우 n이 m의 약수라고 판정한다

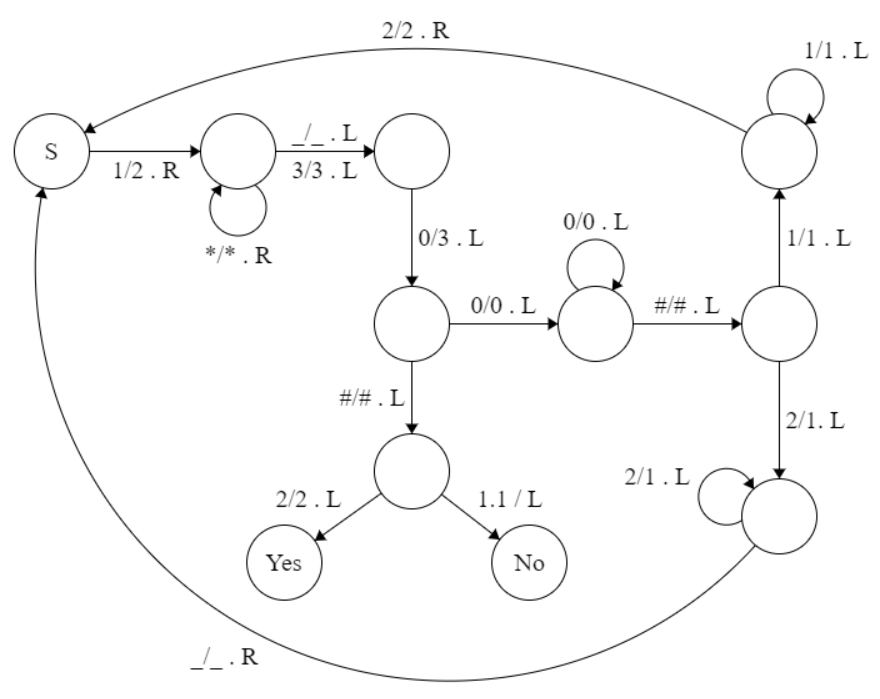
라고 요약할 수 있다. 이를 구현하면 다음과 같다. 와 ㅁㅊ 내가 해냈어 이제 \(1^n\#0^m\)형식의 문자열을 입력받아 위 흐름을 따라가면, 도달하는 지점이 Yes인지 No인지에 따라 n이 m의 약수인지 여부를 판별할 수 있다.

Step 2. 문자열 전처리

그런데 입력 문자열은 \(w=0^p\)만이 들어온다. 따라서 이를 다루기 편한(?) \(1^n\#0^m\)형태로 바꾸기 위해 전처리 로직을 만들어야 한다. 전처리 로직에서는 입력 문자열의 왼쪽에 “\(1^n\#\)”를 이어붙이는 역할을 수행하며, 효율성을 고려해 n은 p/2(처음 0 개수의 절반)로 설정했다. 전처리가 완료되면 begin(실질적 시작점)으로 이동한다.

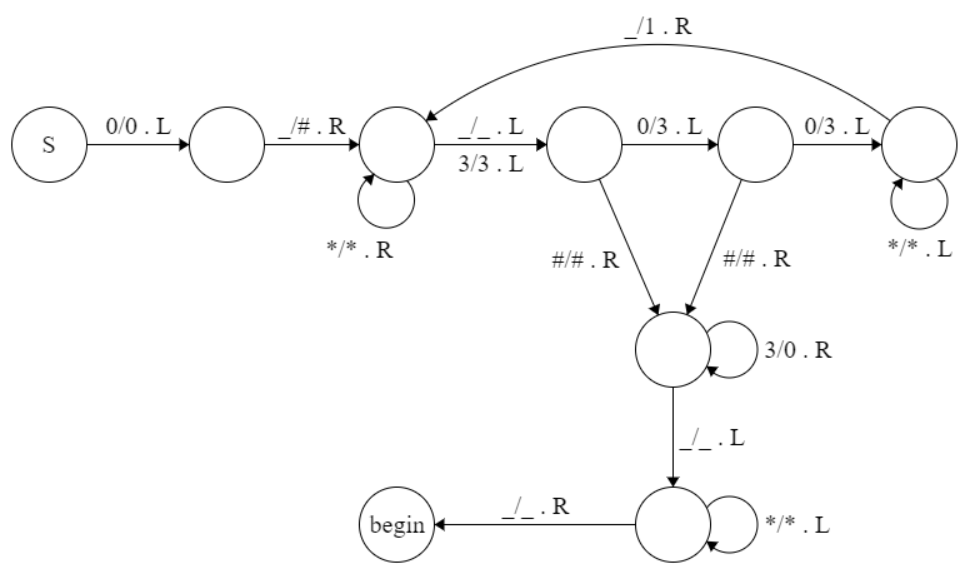
Step 3. 소수 판별

이제 준비가 거의 끝났다. 전처리기와 약수 판별기가 있으므로 다음과 같은 로직을 수행할 수 있다.

  1. 전처리를 수행해 문자열을 “11…1#00…0”으로 바꾼다
  2. 만들어진 \(1^n\#0^p\) 문자열에서 n이 p의 약수인지 확인한다.
  3. 약수가 아니라고 판정되면 제일 왼쪽의 1을 하나 지우고(n-=1), 다시 1. 로 돌아간다
  4. 약수라고 판정되면 n=1인지 확인한다.

p는 p/2 이하의 약수를 적어도 하나(=1) 가지므로 이 로직은 언젠가 3. 에 도달하게 되고, 이때 n=1인지 여부를 판정함으로써 p가 소수인지 판별할 수 있다. 이를 튜링머신으로 표현하면 아래와 같다.

  • S : 실제 시작점
  • begin : 전처리 종료 후 도달상태 = step1 튜링머신의 시작점 S
  • Yes, No : step1 튜링머신에서의 Yes, No 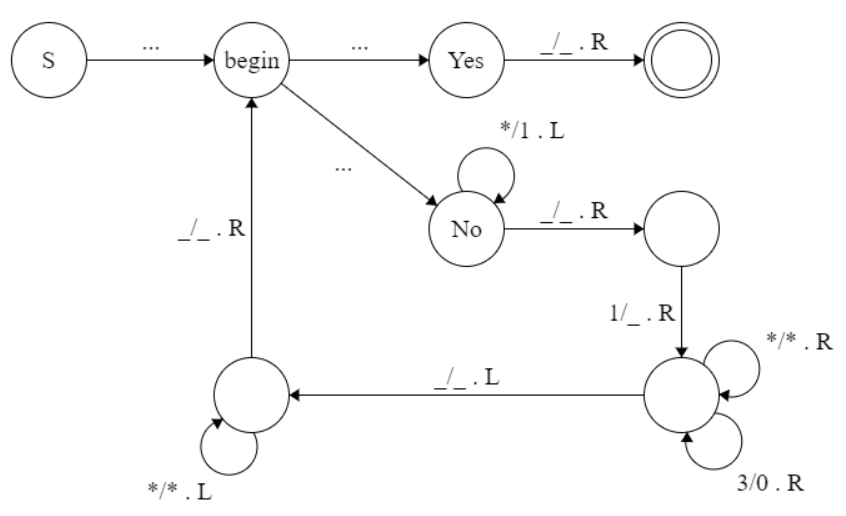위 그림에서 ◎가 전체 튜링머신의 유일한 accept state가 된다.